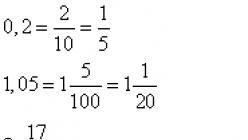In der trockenen mathematischen Sprache ist ein Bruch eine Zahl, die als Teil von Eins dargestellt wird. Brüche werden im menschlichen Leben häufig verwendet: Wir verwenden Brüche, um Proportionen in kulinarischen Rezepten anzugeben, dezimale Punkte bei Wettbewerben zu vergeben oder sie zur Berechnung von Rabatten in Geschäften zu verwenden.

Darstellung von Brüchen

Es gibt mindestens zwei Formen, eine Bruchzahl zu schreiben: in Dezimalform oder in Form eines gewöhnlichen Bruchs. In Dezimalform sehen die Zahlen wie 0,5 aus; 0,25 oder 1,375. Wir können jeden dieser Werte als gewöhnlichen Bruch darstellen:

• 0,5 = 1/2;
• 0,25 = 1/4;
• 1,375 = 11/8.

Und wenn wir 0,5 und 0,25 leicht von einem gewöhnlichen Bruch in eine Dezimalzahl und zurück umwandeln, dann ist im Fall der Zahl 1,375 nicht alles offensichtlich. Wie kann man eine Dezimalzahl schnell in einen Bruch umwandeln? Es gibt drei einfache Möglichkeiten.

Das Komma loswerden

Der einfachste Algorithmus besteht darin, eine Zahl mit 10 zu multiplizieren, bis das Komma aus dem Zähler verschwindet. Diese Transformation erfolgt in drei Schritten:

Schritt 1: Zunächst schreiben wir die Dezimalzahl als Bruch „Zahl/1“, d. h. wir erhalten 0,5/1; 0,25/1 und 1,375/1.

Schritt 2: Danach multiplizieren Sie Zähler und Nenner der neuen Brüche, bis das Komma aus den Zählern verschwindet:

• 0,5/1 = 5/10;
• 0,25/1 = 2,5/10 = 25/100;
• 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.

Schritt 3: Wir reduzieren die resultierenden Fraktionen auf eine verdauliche Form:

• 5/10 = 1 × 5 / 2 × 5 = 1/2;
• 25/100 = 1 × 25 / 4 × 25 = 1/4;
• 1375/1000 = 11 × 125 / 8 × 125 = 11/8.

Die Zahl 1,375 musste dreimal mit 10 multipliziert werden, was nicht mehr sehr praktisch ist, aber was müssen wir tun, wenn wir die Zahl 0,000625 umrechnen müssen? In dieser Situation verwenden wir die folgende Methode zur Umrechnung von Brüchen.

Kommas noch einfacher loswerden

Die erste Methode beschreibt ausführlich den Algorithmus zum „Entfernen“ eines Kommas aus einer Dezimalzahl, aber wir können diesen Prozess vereinfachen. Auch hier folgen wir drei Schritten.

Schritt 1: Wir zählen, wie viele Nachkommastellen es gibt. Beispielsweise hat die Zahl 1,375 drei solcher Ziffern und 0,000625 sechs. Diese Größe bezeichnen wir mit dem Buchstaben n.

Schritt 2: Jetzt müssen wir den Bruch nur noch in der Form C/10 n darstellen, wobei C die signifikanten Ziffern des Bruchs sind (ohne Nullen, falls vorhanden) und n die Anzahl der Nachkommastellen ist. Z.B:

• für die Zahl 1,375 C = 1375, n = 3, der Endbruch nach der Formel 1375/10 3 = 1375/1000;
• für die Zahl 0,000625 C = 625, n = 6, der Endbruch nach der Formel 625/10 6 = 625/1000000.

Im Wesentlichen ist 10n eine 1 mit n Nullen, sodass Sie sich nicht die Mühe machen müssen, die Zehn zu potenzieren – nur 1 mit n Nullen. Danach ist es ratsam, einen Bruch, der so reich an Nullen ist, zu kürzen.

Schritt 3: Wir reduzieren die Nullen und erhalten das Endergebnis:

• 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
• 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.

Der Bruch 11/8 ist ein unechter Bruch, weil sein Zähler größer als sein Nenner ist, was bedeutet, dass wir den ganzen Teil isolieren können. In dieser Situation subtrahieren wir den ganzen Teil von 8/8 von 11/8 und erhalten den Rest 3/8, daher sieht der Bruch wie 1 und 3/8 aus.

Konvertierung nach Gehör

Wer Dezimalzahlen richtig lesen kann, kann sie am einfachsten durch Hören umrechnen. Wenn Sie 0,025 nicht als „Null, Null, Fünfundzwanzig“, sondern als „25 Tausendstel“ lesen, haben Sie kein Problem damit, Dezimalzahlen in Brüche umzuwandeln.

0,025 = 25/1000 = 1/40

Wenn Sie also eine Dezimalzahl richtig lesen, können Sie sie sofort als Bruch aufschreiben und bei Bedarf kürzen.

Beispiele für die Verwendung von Brüchen im Alltag

Auf den ersten Blick werden gewöhnliche Brüche im Alltag oder bei der Arbeit praktisch nicht verwendet, und es ist schwer, sich eine Situation vorzustellen, in der man außerhalb von Schulaufgaben einen Dezimalbruch in einen regelmäßigen Bruch umwandeln muss. Schauen wir uns ein paar Beispiele an.

Arbeit

Sie arbeiten also in einem Süßwarenladen und verkaufen Halva nach Gewicht. Um den Verkauf des Produkts zu erleichtern, teilt man die Halva in Kilogrammbriketts auf, aber nur wenige Käufer sind bereit, ein ganzes Kilogramm zu kaufen. Daher müssen Sie den Leckerbissen jedes Mal in Stücke teilen. Und wenn der nächste Käufer Sie um 0,4 kg Halva bittet, verkaufen Sie ihm problemlos die benötigte Portion.

0,4 = 4/10 = 2/5

Leben

Sie müssen beispielsweise eine 12-prozentige Lösung herstellen, um das Modell im gewünschten Farbton zu lackieren. Dazu müssen Sie Farbe und Lösungsmittel mischen, aber wie macht man das richtig? 12 % ist ein Dezimalbruch von 0,12. Wandeln Sie die Zahl in einen gemeinsamen Bruch um und erhalten Sie:

0,12 = 12/100 = 3/25

Wenn Sie die Fraktionen kennen, können Sie die Zutaten richtig mischen und die gewünschte Farbe erhalten.

Abschluss

Brüche werden im Alltag häufig verwendet. Wenn Sie also häufig Dezimalzahlen in Brüche umrechnen müssen, sollten Sie einen Online-Rechner verwenden, der das Ergebnis sofort als gekürzten Bruch liefert.

Nicht nur viele Studierende fragen sich, wie man einen Bruch in eine Zahl umwandelt. Dafür gibt es mehrere recht einfache und verständliche Möglichkeiten. Die Wahl einer bestimmten Methode hängt von den Präferenzen des Entscheiders ab.

Zunächst müssen Sie wissen, wie Brüche geschrieben werden. Und sie sind wie folgt geschrieben:

1. Normal. Es wird mit Zähler und Nenner unter Verwendung einer Schräge oder einer Spalte (1/2) geschrieben.
2. Dezimal. Es wird durch Kommas getrennt geschrieben (1.0, 2.5 usw.).

Bevor Sie mit dem Lösen beginnen, müssen Sie wissen, was ein unechter Bruch ist, da er recht häufig vorkommt. Der Zähler ist größer als der Nenner, zum Beispiel 15/6. Auch unechte Brüche können auf diese Weise ohne Aufwand und ohne Zeitaufwand gelöst werden.

Eine gemischte Zahl liegt vor, wenn das Ergebnis eine ganze Zahl und ein Bruchteil ist, zum Beispiel 52/3.

Jede natürliche Zahl kann als Bruch mit völlig unterschiedlichen natürlichen Nennern geschrieben werden, zum Beispiel: 1= 2/2=3/3 = usw.

Sie können auch mit einem Taschenrechner übersetzen, allerdings verfügen nicht alle über diese Funktion. Es gibt einen speziellen technischen Rechner, der über eine solche Funktion verfügt, aber insbesondere in der Schule ist es nicht immer möglich, ihn zu verwenden. Daher ist es besser, dieses Thema zu verstehen.

Das erste, worauf Sie achten sollten, ist, um welchen Bruch es sich handelt. Wenn es leicht mit den gleichen Werten wie der Zähler bis zu 10 multipliziert werden kann, können Sie die erste Methode verwenden. Beispiel: Sie multiplizieren eine gewöhnliche ½ im Zähler und Nenner mit 5 und erhalten 5/10, was als 0,5 geschrieben werden kann.

Diese Regel basiert auf der Tatsache, dass eine Dezimalzahl im Nenner immer einen runden Wert hat, beispielsweise 10,100,1000 usw.

Daraus folgt: Wenn Sie Zähler und Nenner multiplizieren, müssen Sie durch die Multiplikation genau den gleichen Wert im Nenner erhalten, unabhängig davon, was im Zähler herauskommt.

Denken Sie daran, dass einige Brüche nicht umgerechnet werden können. Dazu müssen Sie dies überprüfen, bevor Sie mit der Lösung beginnen.

Zum Beispiel: 1,3333, wobei die Zahl 3 bis ins Unendliche wiederholt wird und der Rechner sie auch nicht loswird. Die einzige Lösung für dieses Problem besteht darin, es nach Möglichkeit auf eine ganze Zahl zu runden. Wenn dies nicht möglich ist, sollten Sie zum Anfang des Beispiels zurückkehren und die Richtigkeit der Lösung des Problems überprüfen, möglicherweise ist ein Fehler aufgetreten.

Abbildung 1-3. Brüche durch Multiplikation umwandeln.

Um die beschriebenen Informationen zu konsolidieren, betrachten Sie das folgende Übersetzungsbeispiel:

1. Beispielsweise müssen Sie 6/20 in eine Dezimalzahl umrechnen. Der erste Schritt besteht darin, es zu überprüfen, wie in Abbildung 1 dargestellt.
2. Erst wenn Sie davon überzeugt sind, dass es zerlegt werden kann, wie in diesem Fall in 2 und 5, sollten Sie mit der eigentlichen Übersetzung beginnen.
3. Die einfachste Möglichkeit wäre, den Nenner zu multiplizieren, um ein Ergebnis von 100 zu erhalten, also 5, da 20x5=100.
4. Folgt man dem Beispiel in Abbildung 2, beträgt das Ergebnis 0,3.

Sie können das Ergebnis konsolidieren und alles noch einmal gemäß Abbildung 3 überprüfen. Um das Thema vollständig zu verstehen und nicht mehr auf das Studium dieses Materials zurückzugreifen. Dieses Wissen wird nicht nur dem Kind, sondern auch dem Erwachsenen helfen.

Übersetzung nach Abteilung

Die zweite Möglichkeit zur Umrechnung von Brüchen ist etwas komplizierter, aber beliebter. Diese Methode wird hauptsächlich von Lehrern in Schulen zur Erklärung verwendet. Insgesamt ist es viel einfacher zu erklären und schneller zu verstehen.

Denken Sie daran, dass Sie zur korrekten Umwandlung eines einfachen Bruchs seinen Zähler durch seinen Nenner dividieren müssen. Wenn man darüber nachdenkt, ist die Lösung schließlich der Prozess der Teilung.

Um diese einfache Regel zu verstehen, müssen Sie die folgende Beispiellösung betrachten:

1. Nehmen wir 78/200, das in eine Dezimalzahl umgewandelt werden muss. Teilen Sie dazu 78 durch 200, also den Zähler durch den Nenner.
2. Aber bevor Sie beginnen, lohnt es sich, einen Blick darauf zu werfen, wie in Abbildung 4 dargestellt.
3. Sobald Sie davon überzeugt sind, dass das Problem gelöst werden kann, sollten Sie mit dem Prozess beginnen. Dazu lohnt es sich, in einer Spalte oder Ecke den Zähler durch den Nenner zu dividieren, wie in Abbildung 5 dargestellt. In Grundschulen wird eine solche Division gelehrt, und es sollte dabei keine Schwierigkeiten geben.

Abbildung 6 zeigt Beispiele der gängigsten Beispiele, die Sie sich einfach merken können, um bei Bedarf keine Zeit mit dem Lösen zu verschwenden. Schließlich wird in der Schule für jede Prüfung oder selbstständige Arbeit nur wenig Zeit zum Lösen eingeräumt, Sie sollten diese also nicht mit etwas verschwenden, das Sie lernen und sich einfach merken können.

Zinsübertragung

Auch die Umrechnung von Prozentsätzen in Dezimalzahlen ist recht einfach. Der Unterricht beginnt in der 5. Klasse, in manchen Schulen sogar schon früher. Aber wenn Ihr Kind dieses Thema im Mathematikunterricht nicht verstanden hat, können Sie es ihm noch einmal anschaulich erklären. Zunächst sollten Sie die Definition eines Prozentsatzes lernen.

Ein Prozentsatz ist ein Hundertstel einer Zahl, also völlig willkürlich. Aus 100 wird beispielsweise 1 und so weiter.

Abbildung 7 zeigt ein anschauliches Beispiel für die Zinsumrechnung.

Um einen Prozentsatz umzurechnen, müssen Sie lediglich das %-Zeichen entfernen und ihn dann durch 100 dividieren.

Ein weiteres Beispiel ist in Abbildung 8 dargestellt.

Wenn Sie eine umgekehrte „Konvertierung“ durchführen müssen, müssen Sie genau umgekehrt vorgehen. Mit anderen Worten: Die Zahl muss mit einhundert multipliziert und dann ein Prozentzeichen hinzugefügt werden.

Und um das Übliche in Prozente umzurechnen, können Sie auch dieses Beispiel nutzen. Sie sollten den Bruch zunächst nur in eine Zahl umwandeln und erst dann in einen Prozentsatz.

Anhand des oben Gesagten können Sie das Prinzip der Übersetzung leicht verstehen. Mit diesen Methoden können Sie einem Kind ein Thema erklären, wenn es es nicht verstanden hat oder zum Zeitpunkt des Unterrichts nicht anwesend war.

Und es wird nie nötig sein, einen Nachhilfelehrer zu engagieren, der Ihrem Kind erklärt, wie man einen Bruch in eine Zahl oder einen Prozentsatz umwandelt.

Dezimalzahlen wie 0,2; 1,05; 3.017 usw. wie sie gehört werden, so werden sie geschrieben. Null Komma zwei, wir bekommen einen Bruchteil. Ein Komma fünf Hundertstel, wir bekommen einen Bruchteil. Drei Komma siebzehn Tausendstel, wir bekommen den Bruchteil. Die Zahlen vor dem Dezimalpunkt sind der ganze Teil des Bruchs. Die Zahl nach dem Komma ist der Zähler des zukünftigen Bruchs. Bei einer einstelligen Zahl nach dem Dezimalpunkt ist der Nenner 10, bei einer zweistelligen Zahl 100, bei einer dreistelligen Zahl 1000 usw. Einige resultierende Brüche können gekürzt werden. In unseren Beispielen

Einen Bruch in eine Dezimalzahl umwandeln

Dies ist die Umkehrung der vorherigen Transformation. Was ist das Merkmal eines Dezimalbruchs? Sein Nenner ist immer 10 oder 100 oder 1000 oder 10000 und so weiter. Wenn Ihr gemeinsamer Bruch einen solchen Nenner hat, ist das kein Problem. Zum Beispiel, oder

Wenn der Bruch zum Beispiel ist. In diesem Fall ist es notwendig, die Grundeigenschaft eines Bruchs zu nutzen und den Nenner in 10 oder 100 oder 1000 umzuwandeln... Wenn wir in unserem Beispiel Zähler und Nenner mit 4 multiplizieren, erhalten wir einen Bruch, der sein kann geschrieben als Dezimalzahl 0,12.

Manche Brüche lassen sich leichter dividieren als den Nenner umrechnen. Zum Beispiel,

Manche Brüche können nicht in Dezimalzahlen umgewandelt werden!
Zum Beispiel,

Einen gemischten Bruch in einen unechten Bruch umwandeln

Ein gemischter Bruch kann beispielsweise leicht in einen unechten Bruch umgewandelt werden. Dazu müssen Sie den ganzen Teil mit dem Nenner (unten) multiplizieren und mit dem Zähler (oben) addieren, wobei der Nenner (unten) unverändert bleibt. Also

Wenn Sie einen gemischten Bruch in einen unechten Bruch umwandeln, können Sie daran denken, dass Sie die Bruchaddition verwenden können

Einen unechten Bruch in einen gemischten Bruch umwandeln (den ganzen Teil hervorheben)

Ein unechter Bruch kann durch Markieren des ganzen Teils in einen gemischten Bruch umgewandelt werden. Schauen wir uns ein Beispiel an. Wir bestimmen, wie viele ganze Zahlen mal „3“ in „23“ passen. Oder dividieren Sie 23 durch 3 auf einem Taschenrechner, die ganze Zahl auf den Dezimalpunkt genau ist die gewünschte. Das ist „7“. Als nächstes bestimmen wir den Zähler des zukünftigen Bruchs: Wir multiplizieren die resultierende „7“ mit dem Nenner „3“ und subtrahieren das Ergebnis vom Zähler „23“. Es ist, als würden wir den Überschuss finden, der vom Zähler „23“ übrig bleibt, wenn wir den Höchstbetrag von „3“ entfernen. Wir lassen den Nenner unverändert. Alles ist erledigt, notieren Sie das Ergebnis

Beim Versuch, mathematische Probleme mit Brüchen zu lösen, stellt ein Schüler fest, dass ihm allein der Wunsch, diese Probleme zu lösen, nicht ausreicht. Kenntnisse im Rechnen mit Bruchzahlen sind ebenfalls erforderlich. Bei einigen Problemen werden alle Anfangsdaten in der Bedingung in Bruchform angegeben. In anderen Fällen kann es sich bei einigen um Brüche und bei anderen um ganze Zahlen handeln. Um mit diesen gegebenen Werten Berechnungen durchführen zu können, müssen Sie diese zunächst in eine einzige Form bringen, also ganze Zahlen in Brüche umwandeln, und dann die Berechnungen durchführen. Im Allgemeinen ist die Umwandlung einer ganzen Zahl in einen Bruch sehr einfach. Dazu müssen Sie die angegebene Zahl selbst in den Zähler des letzten Bruchs und eine in seinen Nenner schreiben. Das heißt, wenn Sie die Zahl 12 in einen Bruch umwandeln müssen, ist der resultierende Bruch 12/1.

Solche Modifikationen helfen dabei, Brüche auf einen gemeinsamen Nenner zu bringen. Dies ist notwendig, um Brüche subtrahieren oder addieren zu können. Beim Multiplizieren und Dividieren ist kein gemeinsamer Nenner erforderlich. Sie können sich ein Beispiel dafür ansehen, wie man eine Zahl in einen Bruch umwandelt und dann zwei Brüche addiert. Nehmen wir an, Sie müssen die Zahl 12 und die Bruchzahl 3/4 addieren. Der erste Term (Nummer 12) wird auf die Form 12/1 reduziert. Allerdings ist sein Nenner gleich 1, während der des zweiten Termes gleich 4 ist. Um diese beiden Brüche weiter zu addieren, müssen sie auf einen gemeinsamen Nenner gebracht werden. Da eine der Zahlen den Nenner 1 hat, ist dies im Allgemeinen einfach. Sie müssen den Nenner der zweiten Zahl nehmen und sowohl den Zähler als auch den Nenner der ersten Zahl damit multiplizieren.

Das Ergebnis der Multiplikation ist: 12/1=48/4. Wenn Sie 48 durch 4 dividieren, erhalten Sie 12, was bedeutet, dass der Bruch auf den richtigen Nenner reduziert wurde. Auf diese Weise können Sie auch verstehen, wie man einen Bruch in eine ganze Zahl umwandelt. Dies gilt nur für unechte Brüche, da der Zähler größer als der Nenner ist. In diesem Fall wird der Zähler durch den Nenner dividiert und wenn kein Rest vorhanden ist, ergibt sich eine ganze Zahl. Mit einem Rest bleibt der Bruch ein Bruch, wobei jedoch der ganze Teil hervorgehoben wird. Nun zur Reduktion auf einen gemeinsamen Nenner im betrachteten Beispiel. Wäre der Nenner des ersten Termes gleich einer anderen Zahl als 1, müssten Zähler und Nenner der ersten Zahl mit dem Nenner der zweiten Zahl und Zähler und Nenner der zweiten Zahl mit dem Nenner der Zahl multipliziert werden Erste.

Beide Begriffe werden auf ihren gemeinsamen Nenner gebracht und stehen zur Addition bereit. Es stellt sich heraus, dass Sie in dieser Aufgabe zwei Zahlen addieren müssen: 48/4 und 3/4. Wenn Sie zwei Brüche mit demselben Nenner addieren, müssen Sie nur deren oberen Teile, also die Zähler, addieren. Der Nenner des Betrags bleibt unverändert. In diesem Beispiel sollte es 48/4+3/4=(48+3)/4=51/4 sein. Dies wird das Ergebnis der Addition sein. Aber in der Mathematik ist es üblich, unechte Brüche in richtige Brüche zu reduzieren. Wir haben oben besprochen, wie man einen Bruch in eine Zahl umwandelt, aber in diesem Beispiel erhalten Sie aus dem Bruch 51/4 keine ganze Zahl, da die Zahl 51 nicht ohne Rest durch die Zahl 4 teilbar ist. Daher müssen Sie trennen der ganzzahlige Teil dieses Bruchs und sein Bruchteil. Der ganzzahlige Teil ist die Zahl, die man erhält, wenn man die erste Zahl kleiner als 51 durch eine ganze Zahl dividiert.

Das heißt, etwas, das ohne Rest durch 4 geteilt werden kann. Die erste Zahl vor der Zahl 51, die vollständig durch 4 teilbar ist, ist die Zahl 48. Wenn man 48 durch 4 teilt, erhält man die Zahl 12. Das bedeutet, dass der ganzzahlige Teil des gewünschten Bruchs 12 ist. Es bleibt nur noch um den Bruchteil der Zahl zu finden. Der Nenner des Bruchteils bleibt derselbe, also in diesem Fall 4. Um den Zähler eines Bruchs zu ermitteln, müssen Sie vom ursprünglichen Zähler die Zahl subtrahieren, die ohne Rest durch den Nenner dividiert wurde. Im betrachteten Beispiel erfordert dies die Subtraktion der Zahl 48 von der Zahl 51. Das heißt, der Zähler des Bruchteils ist gleich 3. Das Ergebnis der Addition sind 12 ganze Zahlen und 3/4. Dasselbe geschieht beim Subtrahieren von Brüchen. Nehmen wir an, Sie müssen die Bruchzahl 3/4 von der ganzen Zahl 12 subtrahieren. Dazu wird die ganze Zahl 12 in einen Bruchteil 12/1 umgewandelt und dann mit der zweiten Zahl auf einen gemeinsamen Nenner gebracht – 48/4.

Bei gleicher Subtraktion bleibt der Nenner beider Brüche unverändert und die Subtraktion erfolgt mit ihren Zählern. Das heißt, der Zähler des zweiten Bruchs wird vom Zähler des ersten Bruchs subtrahiert. In diesem Beispiel wäre es 48/4-3/4=(48-3)/4=45/4. Und wieder haben wir einen unechten Bruch erhalten, der auf einen echten Bruch reduziert werden muss. Um einen ganzen Teil zu isolieren, ermitteln Sie die erste Zahl bis 45, die ohne Rest durch 4 teilbar ist. Dies ist 44. Wenn die Zahl 44 durch 4 geteilt wird, ist das Ergebnis 11. Das bedeutet, dass der ganzzahlige Teil des endgültigen Bruchs gleich 11 ist. Im Bruchteil bleibt auch der Nenner unverändert und der Zähler Vom ursprünglichen unechten Bruch wird die Zahl subtrahiert, die ohne Rest durch den Nenner dividiert wurde. Das heißt, Sie müssen 44 von 45 subtrahieren. Das bedeutet, dass der Zähler im Bruchteil gleich 1 und 12-3/4=11 und 1/4 ist.

Wenn Sie eine ganze Zahl und eine Bruchzahl erhalten, deren Nenner jedoch 10 ist, ist es einfacher, die zweite Zahl in einen Dezimalbruch umzuwandeln und dann die Berechnungen durchzuführen. Beispielsweise müssen Sie die ganze Zahl 12 und die Bruchzahl 3/10 addieren. Wenn Sie 3/10 als Dezimalzahl schreiben, erhalten Sie 0,3. Jetzt ist es viel einfacher, 0,3 zu 12 zu addieren und 2,3 zu erhalten, als Brüche auf einen gemeinsamen Nenner zu bringen, Berechnungen durchzuführen und dann die ganzen und gebrochenen Teile von einem unechten Bruch zu trennen. Selbst die einfachsten Probleme mit Brüchen setzen voraus, dass der Schüler (oder die Schülerin) weiß, wie man eine ganze Zahl in einen Bruch umwandelt. Diese Regeln sind zu einfach und leicht zu merken. Aber mit ihrer Hilfe ist es sehr einfach, Berechnungen von Bruchzahlen durchzuführen.

Wenn wir 497 durch 4 teilen müssen, werden wir bei der Division feststellen, dass 497 nicht gleichmäßig durch 4 teilbar ist, d. h. der Rest der Division bleibt bestehen. In solchen Fällen spricht man von „vollendet“. Division mit Rest, und die Lösung lautet wie folgt:
497: 4 = 124 (1 Rest).

Die Divisionskomponenten auf der linken Seite der Gleichheit heißen genauso wie bei der Division ohne Rest: 497 - Dividende, 4 - Teiler. Das Ergebnis der Division bei Division mit einem Rest wird aufgerufen unvollständig privat. In unserem Fall ist dies die Zahl 124. Und schließlich ist die letzte Komponente, die nicht in der gewöhnlichen Division steht Rest. In Fällen, in denen es keinen Rest gibt, spricht man von der Division einer Zahl durch eine andere spurlos oder vollständig. Es wird angenommen, dass bei einer solchen Division der Rest Null ist. In unserem Fall ist der Rest 1.

Der Rest ist immer kleiner als der Divisor.

Die Division kann durch Multiplikation überprüft werden. Liegt beispielsweise eine Gleichheit 64:32 = 2 vor, dann kann die Prüfung wie folgt erfolgen: 64 = 32 * 2.

In Fällen, in denen eine Division mit einem Rest durchgeführt wird, ist es häufig praktisch, die Gleichheit zu verwenden
a = b * n + r,
Dabei ist a der Dividend, b der Divisor, n der Teilquotient und r der Rest.

Der Quotient natürlicher Zahlen kann als Bruch geschrieben werden.

Der Zähler eines Bruchs ist der Dividend und der Nenner ist der Divisor.

Da der Zähler eines Bruchs der Dividend und der Nenner der Divisor ist, glauben, dass die Gerade eines Bruchs die Aktion der Division bedeutet. Manchmal ist es praktisch, die Division als Bruch zu schreiben, ohne das Zeichen „:“ zu verwenden.

Der Quotient der Division der natürlichen Zahlen m und n kann als Bruch \(\frac(m)(n)\) geschrieben werden, wobei der Zähler m der Dividend und der Nenner n der Divisor ist:
\(m:n = \frac(m)(n)\)

Es gelten folgende Regeln:

Um den Bruch \(\frac(m)(n)\) zu erhalten, müssen Sie die Einheit in n gleiche Teile (Anteile) teilen und m solcher Teile nehmen.

Um den Bruch \(\frac(m)(n)\) zu erhalten, müssen Sie die Zahl m durch die Zahl n dividieren.

Um einen Teil eines Ganzen zu finden, müssen Sie die dem Ganzen entsprechende Zahl durch den Nenner dividieren und das Ergebnis mit dem Zähler des Bruchs multiplizieren, der diesen Teil ausdrückt.

Um aus seinem Teil ein Ganzes zu finden, müssen Sie die diesem Teil entsprechende Zahl durch den Zähler dividieren und das Ergebnis mit dem Nenner des Bruchs multiplizieren, der diesen Teil ausdrückt.

Wenn sowohl Zähler als auch Nenner eines Bruchs mit derselben Zahl (außer Null) multipliziert werden, ändert sich der Wert des Bruchs nicht:
\(\large \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)

Wenn sowohl Zähler als auch Nenner eines Bruchs durch dieselbe Zahl (außer Null) dividiert werden, ändert sich der Wert des Bruchs nicht:
\(\large \frac(a)(b) = \frac(a: m)(b: m) \)
Diese Eigenschaft heißt Haupteigenschaft eines Bruchs.

Die letzten beiden Transformationen werden aufgerufen einen Bruch reduzieren.

Wenn Brüche als Brüche mit demselben Nenner dargestellt werden müssen, wird diese Aktion aufgerufen Brüche auf einen gemeinsamen Nenner reduzieren.

Echte und unechte Brüche. Gemischte Zahlen

Sie wissen bereits, dass man einen Bruch erhalten kann, indem man ein Ganzes in gleiche Teile teilt und mehrere solcher Teile nimmt. Beispielsweise bedeutet der Bruch \(\frac(3)(4)\) drei Viertel eins. In vielen der Aufgaben im vorherigen Absatz wurden Brüche verwendet, um Teile eines Ganzen darzustellen. Der gesunde Menschenverstand schreibt vor, dass der Teil immer kleiner sein sollte als das Ganze, aber was ist mit Brüchen wie \(\frac(5)(5)\) oder \(\frac(8)(5)\)? Es ist klar, dass dies nicht mehr Teil der Einheit ist. Dies ist wahrscheinlich der Grund, warum man Brüche nennt, deren Zähler größer oder gleich dem Nenner ist unechte Brüche. Die restlichen Brüche, also Brüche, deren Zähler kleiner als der Nenner ist, werden aufgerufen richtige Brüche.

Wie Sie wissen, kann man sich jeden gewöhnlichen Bruch, sowohl den echten als auch den unechten Bruch, als das Ergebnis der Division des Zählers durch den Nenner vorstellen. Daher bedeutet der Begriff „unechter Bruch“ in der Mathematik im Gegensatz zur gewöhnlichen Sprache nicht, dass wir etwas falsch gemacht haben, sondern nur, dass der Zähler dieses Bruchs größer oder gleich dem Nenner ist.

Besteht eine Zahl aus einem ganzzahligen Teil und einem Bruch, dann ist z Brüche heißen gemischt.

Zum Beispiel:
\(5:3 = 1\frac(2)(3) \) : 1 ist der ganzzahlige Teil und \(\frac(2)(3) \) ist der Bruchteil.

Wenn der Zähler des Bruchs \(\frac(a)(b)\) durch eine natürliche Zahl n teilbar ist, dann muss, um diesen Bruch durch n zu teilen, sein Zähler durch diese Zahl geteilt werden:
\(\large \frac(a)(b) : n = \frac(a:n)(b) \)

Wenn der Zähler des Bruchs \(\frac(a)(b)\) nicht durch eine natürliche Zahl n teilbar ist, müssen Sie zum Teilen dieses Bruchs durch n seinen Nenner mit dieser Zahl multiplizieren:
\(\large \frac(a)(b) : n = \frac(a)(bn) \)

Beachten Sie, dass die zweite Regel auch gilt, wenn der Zähler durch n teilbar ist. Daher können wir es verwenden, wenn es schwierig ist, auf den ersten Blick festzustellen, ob der Zähler eines Bruchs durch n teilbar ist oder nicht.

Aktionen mit Brüchen. Brüche addieren.

Sie können mit Bruchzahlen arithmetische Operationen durchführen, genau wie mit natürlichen Zahlen. Schauen wir uns zunächst das Addieren von Brüchen an. Es ist einfach, Brüche mit gleichen Nennern zu addieren. Finden wir zum Beispiel die Summe von \(\frac(2)(7)\) und \(\frac(3)(7)\). Es ist leicht zu verstehen, dass \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \)

Um Brüche mit demselben Nenner zu addieren, müssen Sie deren Zähler addieren und den Nenner gleich lassen.

Unter Verwendung von Buchstaben kann die Regel zum Addieren von Brüchen mit gleichem Nenner wie folgt geschrieben werden:
\(\large \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)

Wenn Sie Brüche mit unterschiedlichen Nennern addieren müssen, müssen diese zunächst auf einen gemeinsamen Nenner reduziert werden. Zum Beispiel:
\(\large \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3 ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)

Für Brüche gelten wie für natürliche Zahlen die kommutativen und assoziativen Eigenschaften der Addition.

Gemischte Brüche addieren

Es werden Notationen wie \(2\frac(2)(3)\) aufgerufen gemischte Brüche. In diesem Fall wird die Nummer 2 aufgerufen ganzer Teil gemischter Bruch, und die Zahl \(\frac(2)(3)\) ist sein Bruchteil. Der Eintrag \(2\frac(2)(3)\) lautet wie folgt: „zwei und zwei Drittel.“

Wenn man die Zahl 8 durch die Zahl 3 dividiert, erhält man zwei Antworten: \(\frac(8)(3)\) und \(2\frac(2)(3)\). Sie drücken dieselbe Bruchzahl aus, d. h. \(\frac(8)(3) = 2 \frac(2)(3)\)

Somit wird der unechte Bruch \(\frac(8)(3)\) als gemischter Bruch \(2\frac(2)(3)\) dargestellt. In solchen Fällen spricht man von einem unechten Bruch den ganzen Teil hervorgehoben.

Subtrahieren von Brüchen (Bruchzahlen)

Die Subtraktion von Bruchzahlen wird wie natürliche Zahlen auf der Grundlage der Additionswirkung bestimmt: Eine andere von einer Zahl zu subtrahieren bedeutet, eine Zahl zu finden, die, wenn man sie zur zweiten addiert, die erste ergibt. Zum Beispiel:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) da \(\frac(7)(9)+\frac(1)(9 ) = \frac(8)(9)\)

Die Regel zum Subtrahieren von Brüchen mit gleichem Nenner ähnelt der Regel zum Addieren solcher Brüche:
Um die Differenz zwischen Brüchen mit demselben Nenner zu ermitteln, müssen Sie den Zähler des zweiten vom Zähler des ersten Bruchs subtrahieren und den Nenner gleich lassen.

Mit Buchstaben wird diese Regel wie folgt geschrieben:
\(\large \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)

Brüche multiplizieren

Um einen Bruch mit einem Bruch zu multiplizieren, müssen Sie deren Zähler und Nenner multiplizieren und das erste Produkt als Zähler und das zweite als Nenner schreiben.

Mit Buchstaben lässt sich die Regel zur Multiplikation von Brüchen wie folgt formulieren:
\(\large \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)

Mit der formulierten Regel können Sie einen Bruch mit einer natürlichen Zahl, mit einem gemischten Bruch und auch mit gemischten Brüchen multiplizieren. Dazu müssen Sie eine natürliche Zahl als Bruch mit dem Nenner 1, einen gemischten Bruch, als unechten Bruch schreiben.

Das Ergebnis der Multiplikation sollte (wenn möglich) vereinfacht werden, indem der Bruch reduziert und der ganze Teil des unechten Bruchs isoliert wird.

Für Brüche gelten wie für natürliche Zahlen die kommutativen und kombinativen Eigenschaften der Multiplikation sowie die Verteilungseigenschaft der Multiplikation relativ zur Addition.

Division von Brüchen

Nehmen wir den Bruch \(\frac(2)(3)\) und „drehen“ ihn um, indem wir Zähler und Nenner vertauschen. Wir erhalten den Bruch \(\frac(3)(2)\). Dieser Bruch heißt umkehren Brüche \(\frac(2)(3)\).

Wenn wir nun den Bruch \(\frac(3)(2)\) „umkehren“, erhalten wir den ursprünglichen Bruch \(\frac(2)(3)\). Daher heißen Brüche wie \(\frac(2)(3)\) und \(\frac(3)(2)\). gegenseitig umgekehrt.

Zum Beispiel die Brüche \(\frac(6)(5) \) und \(\frac(5)(6) \), \(\frac(7)(18) \) und \(\frac (18). )(7)\).

Mit Buchstaben können Kehrbrüche wie folgt geschrieben werden: \(\frac(a)(b) \) und \(\frac(b)(a) \)

Es ist klar, dass das Produkt der reziproken Brüche ist gleich 1. Zum Beispiel: \(\frac(2)(3) \cdot \frac(3)(2) =1 \)

Mithilfe reziproker Brüche können Sie die Division von Brüchen auf die Multiplikation reduzieren.

Die Regel zum Teilen eines Bruchs durch einen Bruch lautet:
Um einen Bruch durch einen anderen zu dividieren, müssen Sie den Dividenden mit dem Kehrwert des Divisors multiplizieren.

Unter Verwendung von Buchstaben kann die Regel zum Teilen von Brüchen wie folgt geschrieben werden:
\(\large \frac(a)(b) : \frac(c)(d) = \frac(a)(b) \cdot \frac(d)(c) \)

Wenn der Dividend oder Divisor eine natürliche Zahl oder ein gemischter Bruch ist, muss er, um die Regel zum Teilen von Brüchen anwenden zu können, zunächst als unechter Bruch dargestellt werden.