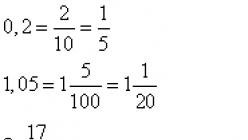In dry mathematical language, a fraction is a number that is represented as a part of one. Fractions are widely used in human life: we use fractions to indicate proportions in culinary recipes, give decimal scores in competitions, or use them to calculate discounts in stores.

Representation of fractions

There are at least two forms of writing one fractional number: in decimal form or in the form of an ordinary fraction. In decimal form, the numbers look like 0.5; 0.25 or 1.375. We can represent any of these values ​​as an ordinary fraction:

• 0,5 = 1/2;
• 0,25 = 1/4;
• 1,375 = 11/8.

And if we easily convert 0.5 and 0.25 from an ordinary fraction to a decimal and back, then in the case of the number 1.375 everything is not obvious. How to quickly convert any decimal number to a fraction? There are three simple ways.

Getting rid of the comma

The simplest algorithm involves multiplying a number by 10 until the comma disappears from the numerator. This transformation is carried out in three steps:

Step 1: To begin with, we write the decimal number as a fraction “number/1”, that is, we get 0.5/1; 0.25/1 and 1.375/1.

Step 2: After this, multiply the numerator and denominator of the new fractions until the comma disappears from the numerators:

• 0,5/1 = 5/10;
• 0,25/1 = 2,5/10 = 25/100;
• 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.

Step 3: We reduce the resulting fractions to a digestible form:

• 5/10 = 1 × 5 / 2 × 5 = 1/2;
• 25/100 = 1 × 25 / 4 × 25 = 1/4;
• 1375/1000 = 11 × 125 / 8 × 125 = 11/8.

The number 1.375 had to be multiplied by 10 three times, which is no longer very convenient, but what do we have to do if we need to convert the number 0.000625? In this situation, we use the following method of converting fractions.

Getting rid of commas even easier

The first method describes in detail the algorithm for “removing” a comma from a decimal, but we can simplify this process. Again, we follow three steps.

Step 1: We count how many digits are after the decimal point. For example, the number 1.375 has three such digits, and 0.000625 has six. We will denote this quantity by the letter n.

Step 2: Now we just need to represent the fraction in the form C/10 n, where C are the significant digits of the fraction (without zeros, if any), and n is the number of digits after the decimal point. Eg:

• for the number 1.375 C = 1375, n = 3, the final fraction according to the formula 1375/10 3 = 1375/1000;
• for the number 0.000625 C = 625, n = 6, the final fraction according to the formula 625/10 6 = 625/1000000.

Essentially, 10n is a 1 with n zeros, so you don't have to bother raising the ten to the power - just 1 with n zeros. After this, it is advisable to reduce a fraction so rich in zeros.

Step 3: We reduce the zeros and get the final result:

• 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
• 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.

The fraction 11/8 is an improper fraction because its numerator is greater than its denominator, which means we can isolate the whole part. In this situation, we subtract the whole part of 8/8 from 11/8 and get the remainder 3/8, therefore the fraction looks like 1 and 3/8.

Conversion by ear

For those who can read decimals correctly, the easiest way to convert them is by hearing. If you read 0.025 not as “zero, zero, twenty-five” but as “25 thousandths,” then you will have no problem converting decimals to fractions.

0,025 = 25/1000 = 1/40

Thus, reading a decimal number correctly allows you to immediately write it down as a fraction and reduce it if necessary.

Examples of using fractions in everyday life

At first glance, ordinary fractions are practically not used in everyday life or at work, and it is difficult to imagine a situation when you need to convert a decimal fraction into a regular fraction outside of school tasks. Let's look at a couple of examples.

Job

So, you work in a candy store and sell halva by weight. To make the product easier to sell, you divide the halva into kilogram briquettes, but few buyers are willing to purchase a whole kilogram. Therefore, you have to divide the treat into pieces each time. And if the next buyer asks you for 0.4 kg of halva, you will sell him the required portion without any problems.

0,4 = 4/10 = 2/5

Life

For example, you need to make a 12% solution to paint the model in the shade you want. To do this, you need to mix paint and solvent, but how to do it correctly? 12% is a decimal fraction of 0.12. Convert the number to a common fraction and get:

0,12 = 12/100 = 3/25

Knowing the fractions will help you mix the ingredients correctly and get the color you want.

Conclusion

Fractions are commonly used in everyday life, so if you frequently need to convert decimals to fractions, you'll want to use an online calculator that can instantly get the result as a reduced fraction.

A large number of students, and not only, are wondering how to convert a fraction into a number. To do this, there are several fairly simple and understandable ways. The choice of a specific method depends on the preferences of the decider.

First of all, you need to know how fractions are written. And they are written as follows:

1. Ordinary. It is written with the numerator and denominator using a slant or a column (1/2).
2. Decimal. It is written separated by commas (1.0, 2.5, and so on).

Before you start solving, you need to know what an improper fraction is, because it occurs quite often. It has a numerator greater than the denominator, for example, 15/6. Improper fractions can also be solved in these ways, without any effort or time.

A mixed number is when the result is a whole number and a fractional part, for example 52/3.

Any natural number can be written as a fraction with completely different natural denominators, for example: 1= 2/2=3/3 = etc.

You can also translate using a calculator, but not all of them have this function. There is a special engineering calculator that has such a function, but it is not always possible to use it, especially at school. Therefore, it is better to understand this topic.

The first thing you should pay attention to is what fraction it is. If it can be easily multiplied up to 10 by the same values ​​as the numerator, then you can use the first method. For example: you multiply an ordinary ½ in the numerator and denominator by 5 and get 5/10, which can be written as 0.5.

This rule is based on the fact that a decimal always has a round value in its denominator, such as 10,100,1000, and so on.

It follows from this that if you multiply the numerator and the denominator, then you need to achieve exactly the same value in the denominator as a result of the multiplication, regardless of what comes out in the numerator.

It is worth remembering that some fractions cannot be converted; to do this, you need to check it before starting the solution.

For example: 1.3333, where the number 3 is repeated ad infinitum, and the calculator will not get rid of it either. The only solution to this problem is to round it to a whole number, if possible. If this is not possible, then you should return to the beginning of the example and check the correctness of the solution to the problem; perhaps an error was made.

Figure 1-3. Converting fractions by multiplication.

To consolidate the described information, consider the following translation example:

1. For example, you need to convert 6/20 to a decimal. The first step is to check it, as shown in Figure 1.
2. Only after you are convinced that it can be decomposed, as in this case into 2 and 5, should you begin the translation itself.
3. The simplest option would be to multiply the denominator to get a result of 100, which is 5, since 20x5=100.
4. Following the example in Figure 2, the result will be 0.3.

You can consolidate the result and review everything again according to Figure 3. In order to fully understand the topic and no longer resort to studying this material. This knowledge will help not only the child, but also the adult.

Translation by division

The second option for converting fractions is a little more complicated, but more popular. This method is mainly used by teachers in schools to explain. Overall, it is much easier to explain and quicker to understand.

It is worth remembering that to correctly convert a simple fraction, you must divide its numerator by its denominator. After all, if you think about it, the solution is the process of division.

In order to understand this simple rule, you need to consider the following example solution:

1. Let's take 78/200, which needs to be converted to decimal. To do this, divide 78 by 200, that is, the numerator by the denominator.
2. But before you start, it's worth checking, as shown in Figure 4.
3. Once you are convinced that it can be solved, you should begin the process. To do this, it is worth dividing the numerator by the denominator in a column or corner, as shown in Figure 5. In primary schools, such division is taught, and there should be no difficulties with this.

Figure 6 shows examples of the most common examples; you can simply remember them so that, if necessary, you do not waste time solving them. After all, at school, each test or independent work is given little time to solve, so you shouldn’t waste it on something that you can learn and simply remember.

Interest transfer

Converting percentages to decimals is also quite easy. This begins to be taught in the 5th grade, and in some schools even earlier. But if your child did not understand this topic during a math lesson, you can clearly explain it to him again. First, you should learn the definition of what a percentage is.

A percentage is one hundredth of a number; in other words, it is completely arbitrary. For example, from 100 it will be 1 and so on.

Figure 7 shows a clear example of interest conversion.

To convert a percentage, you just need to remove the % sign and then divide it by 100.

Another example is shown in Figure 8.

If you need to carry out a reverse “conversion”, you need to do everything exactly the opposite. In other words, the number must be multiplied by one hundred and then a percentage symbol must be added.

And in order to convert the usual into percentages, you can also use this example. Only initially should you convert the fraction into a number and only then into a percentage.

Based on the above, you can easily understand the principle of translation. Using these methods, you can explain a topic to a child if he did not understand it or was not present in the lesson at the time of its completion.

And there will never be a need to hire a tutor to explain to your child how to convert a fraction into a number or percentage.

Decimal numbers such as 0.2; 1.05; 3.017, etc. as they are heard, so they are written. Zero point two, we get a fraction. One point five hundredths, we get a fraction. Three point seventeen thousandths, we get the fraction. The numbers before the decimal point are the whole part of the fraction. The number after the decimal point is the numerator of the future fraction. If there is a single-digit number after the decimal point, the denominator will be 10, if there is a two-digit number - 100, a three-digit number - 1000, etc. Some resulting fractions can be reduced. In our examples

Converting a fraction to a decimal

This is the reverse of the previous transformation. What is the characteristic of a decimal fraction? Its denominator is always 10, or 100, or 1000, or 10000, and so on. If your common fraction has a denominator like this, there's no problem. For example, or

If the fraction is, for example . In this case, it is necessary to use the basic property of a fraction and convert the denominator to 10 or 100, or 1000... In our example, if we multiply the numerator and denominator by 4, we get a fraction that can be written as a decimal number 0.12.

Some fractions are easier to divide than to convert the denominator. For example,

Some fractions cannot be converted to decimals!
For example,

Converting a mixed fraction to an improper fraction

A mixed fraction, for example, can be easily converted to an improper fraction. To do this, you need to multiply the whole part by the denominator (bottom) and add it with the numerator (top), leaving the denominator (bottom) unchanged. That is

When converting a mixed fraction to an improper fraction, you can remember that you can use fraction addition

Converting an improper fraction to a mixed fraction (highlighting the whole part)

An improper fraction can be converted to a mixed fraction by highlighting the whole part. Let's look at an example. We determine how many integer times “3” fits into “23”. Or divide 23 by 3 on a calculator, the whole number to the decimal point is the desired one. This is "7". Next, we determine the numerator of the future fraction: we multiply the resulting “7” by the denominator “3” and subtract the result from the numerator “23”. It’s as if we find the extra that remains from the numerator “23” if we remove the maximum amount of “3”. We leave the denominator unchanged. Everything is done, write down the result

When trying to solve mathematical problems with fractions, a student realizes that just the desire to solve these problems is not enough for him. Knowledge of calculations with fractional numbers is also required. In some problems, all initial data are given in the condition in fractional form. In others, some of them may be fractions, and some may be integers. In order to carry out any calculations with these given values, you must first bring them to a single form, that is, convert whole numbers into fractions, and then do the calculations. In general, the way to convert a whole number into a fraction is very simple. To do this, you need to write the given number itself in the numerator of the final fraction, and one in its denominator. That is, if you need to convert the number 12 into a fraction, then the resulting fraction will be 12/1.

Such modifications help bring fractions to a common denominator. This is necessary in order to be able to subtract or add fractions. When multiplying and dividing them, a common denominator is not required. You can look at an example of how to convert a number into a fraction and then add two fractions. Let's say you need to add the number 12 and the fractional number 3/4. The first term (number 12) is reduced to the form 12/1. However, its denominator is equal to 1, while that of the second term is equal to 4. To further add these two fractions, they must be brought to a common denominator. Due to the fact that one of the numbers has a denominator of 1, this is generally easy to do. You need to take the denominator of the second number and multiply by it both the numerator and the denominator of the first.

The result of multiplication is: 12/1=48/4. If you divide 48 by 4, you get 12, which means the fraction has been reduced to the correct denominator. This way you can also understand how to convert a fraction into a whole number. This only applies to improper fractions because they have a numerator greater than the denominator. In this case, the numerator is divided by the denominator and, if there is no remainder, there will be a whole number. With a remainder, the fraction remains a fraction, but with the whole part highlighted. Now regarding reduction to a common denominator in the example considered. If the denominator of the first term were equal to some other number other than 1, the numerator and denominator of the first number would have to be multiplied by the denominator of the second, and the numerator and denominator of the second by the denominator of the first.

Both terms are reduced to their common denominator and ready for addition. It turns out that in this problem you need to add two numbers: 48/4 and 3/4. When adding two fractions with the same denominator, you only need to sum their upper parts, that is, the numerators. The denominator of the amount will remain unchanged. In this example it should be 48/4+3/4=(48+3)/4=51/4. This will be the result of the addition. But in mathematics it is customary to reduce improper fractions to correct ones. We discussed above how to turn a fraction into a number, but in this example you will not get an integer from the fraction 51/4, since the number 51 is not divisible by the number 4 without a remainder. Therefore, you need to separate the integer part of this fraction and its fractional part. The integer part will be the number that is obtained by dividing by an integer the first number less than 51.

That is, something that can be divided by 4 without a remainder. The first number before the number 51, which is completely divisible by 4, will be the number 48. Dividing 48 by 4, the number 12 is obtained. This means that the integer part of the desired fraction will be 12. All that remains is to find the fractional part of the number. The denominator of the fractional part remains the same, that is, 4 in this case. To find the numerator of a fraction, you need to subtract from the original numerator the number that was divided by the denominator without a remainder. In the example under consideration, this requires subtracting the number 48 from the number 51. That is, the numerator of the fractional part is equal to 3. The result of the addition will be 12 integers and 3/4. The same is done when subtracting fractions. Let's say you need to subtract the fractional number 3/4 from the integer 12. To do this, the integer 12 is converted into a fractional 12/1, and then brought to a common denominator with the second number - 48/4.

When subtracting in the same way, the denominator of both fractions remains unchanged, and subtraction is carried out with their numerators. That is, the numerator of the second is subtracted from the numerator of the first fraction. In this example it would be 48/4-3/4=(48-3)/4=45/4. And again we got an improper fraction, which must be reduced to a proper one. To isolate an entire part, determine the first number up to 45, which is divisible by 4 without a remainder. This will be 44. If the number 44 is divided by 4, the result is 11. This means that the integer part of the final fraction is equal to 11. In the fractional part, the denominator is also left unchanged, and from the numerator of the original improper fraction the number that was divided by the denominator without a remainder is subtracted. That is, you need to subtract 44 from 45. This means the numerator in the fractional part is equal to 1 and 12-3/4=11 and 1/4.

If you are given one integer number and one fractional number, but its denominator is 10, then it is easier to convert the second number into a decimal fraction and then carry out the calculations. For example, you need to add the integer 12 and the fractional number 3/10. If you write 3/10 as a decimal, you get 0.3. Now it is much easier to add 0.3 to 12 and get 2.3 than to bring fractions to a common denominator, perform calculations, and then separate the whole and fractional parts from an improper fraction. Even the simplest problems with fractions assume that the student (or student) knows how to convert a whole number into a fraction. These rules are too simple and easy to remember. But with the help of them it is very easy to carry out calculations of fractional numbers.

If we need to divide 497 by 4, then when dividing we will see that 497 is not evenly divisible by 4, i.e. the remainder of the division remains. In such cases it is said that it is completed division with remainder, and the solution is written as follows:
497: 4 = 124 (1 remainder).

The division components on the left side of the equality are called the same as in division without a remainder: 497 - dividend, 4 - divider. The result of division when divided with a remainder is called incomplete private. In our case, this is the number 124. And finally, the last component, which is not in ordinary division, is remainder. In cases where there is no remainder, one number is said to be divided by another without a trace, or completely. It is believed that with such a division the remainder is zero. In our case, the remainder is 1.

The remainder is always less than the divisor.

Division can be checked by multiplication. If, for example, there is an equality 64: 32 = 2, then the check can be done like this: 64 = 32 * 2.

Often in cases where division with a remainder is performed, it is convenient to use the equality
a = b * n + r,
where a is the dividend, b is the divisor, n is the partial quotient, r is the remainder.

The quotient of natural numbers can be written as a fraction.

The numerator of a fraction is the dividend, and the denominator is the divisor.

Since the numerator of a fraction is the dividend and the denominator is the divisor, believe that the line of a fraction means the action of division. Sometimes it is convenient to write division as a fraction without using the ":" sign.

The quotient of the division of natural numbers m and n can be written as a fraction \(\frac(m)(n) \), where the numerator m is the dividend, and the denominator n is the divisor:
\(m:n = \frac(m)(n) \)

The following rules are true:

To get the fraction \(\frac(m)(n)\), you need to divide the unit into n equal parts (shares) and take m such parts.

To get the fraction \(\frac(m)(n)\), you need to divide the number m by the number n.

To find a part of a whole, you need to divide the number corresponding to the whole by the denominator and multiply the result by the numerator of the fraction that expresses this part.

To find a whole from its part, you need to divide the number corresponding to this part by the numerator and multiply the result by the denominator of the fraction that expresses this part.

If both the numerator and denominator of a fraction are multiplied by the same number (except zero), the value of the fraction will not change:
\(\large \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)

If both the numerator and denominator of a fraction are divided by the same number (except zero), the value of the fraction will not change:
\(\large \frac(a)(b) = \frac(a: m)(b: m) \)
This property is called main property of a fraction.

The last two transformations are called reducing a fraction.

If fractions need to be represented as fractions with the same denominator, then this action is called reducing fractions to a common denominator.

Proper and improper fractions. Mixed numbers

You already know that a fraction can be obtained by dividing a whole into equal parts and taking several such parts. For example, the fraction \(\frac(3)(4)\) means three-quarters of one. In many of the problems in the previous paragraph, fractions were used to represent parts of a whole. Common sense dictates that the part should always be less than the whole, but what about fractions such as \(\frac(5)(5)\) or \(\frac(8)(5)\)? It is clear that this is no longer part of the unit. This is probably why fractions whose numerator is greater than or equal to the denominator are called improper fractions. The remaining fractions, i.e. fractions whose numerator is less than the denominator, are called correct fractions.

As you know, any common fraction, both proper and improper, can be thought of as the result of dividing the numerator by the denominator. Therefore, in mathematics, unlike ordinary language, the term “improper fraction” does not mean that we did something wrong, but only that the numerator of this fraction is greater than or equal to the denominator.

If a number consists of an integer part and a fraction, then such fractions are called mixed.

For example:
\(5:3 = 1\frac(2)(3) \) : 1 is the integer part, and \(\frac(2)(3) \) is the fractional part.

If the numerator of the fraction \(\frac(a)(b) \) is divisible by a natural number n, then in order to divide this fraction by n, its numerator must be divided by this number:
\(\large \frac(a)(b) : n = \frac(a:n)(b) \)

If the numerator of the fraction \(\frac(a)(b)\) is not divisible by a natural number n, then to divide this fraction by n, you need to multiply its denominator by this number:
\(\large \frac(a)(b) : n = \frac(a)(bn) \)

Note that the second rule is also true when the numerator is divisible by n. Therefore, we can use it when it is difficult to determine at first glance whether the numerator of a fraction is divisible by n or not.

Actions with fractions. Adding fractions.

You can perform arithmetic operations with fractional numbers, just like with natural numbers. Let's look at adding fractions first. It's easy to add fractions with like denominators. Let us find, for example, the sum of \(\frac(2)(7)\) and \(\frac(3)(7)\). It is easy to understand that \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \)

To add fractions with the same denominators, you need to add their numerators and leave the denominator the same.

Using letters, the rule for adding fractions with like denominators can be written as follows:
\(\large \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)

If you need to add fractions with different denominators, they must first be reduced to a common denominator. For example:
\(\large \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3 ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)

For fractions, as for natural numbers, the commutative and associative properties of addition are valid.

Adding mixed fractions

Notations such as \(2\frac(2)(3)\) are called mixed fractions. In this case, the number 2 is called whole part mixed fraction, and the number \(\frac(2)(3)\) is its fractional part. The entry \(2\frac(2)(3)\) is read as follows: “two and two thirds.”

When dividing the number 8 by the number 3, you can get two answers: \(\frac(8)(3)\) and \(2\frac(2)(3)\). They express the same fractional number, i.e. \(\frac(8)(3) = 2 \frac(2)(3)\)

Thus, the improper fraction \(\frac(8)(3)\) is represented as a mixed fraction \(2\frac(2)(3)\). In such cases they say that from an improper fraction highlighted the whole part.

Subtracting fractions (fractional numbers)

Subtraction of fractional numbers, like natural numbers, is determined on the basis of the action of addition: subtracting another from one number means finding a number that, when added to the second, gives the first. For example:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) since \(\frac(7)(9)+\frac(1)(9 ) = \frac(8)(9)\)

The rule for subtracting fractions with like denominators is similar to the rule for adding such fractions:
To find the difference between fractions with the same denominators, you need to subtract the numerator of the second from the numerator of the first fraction, and leave the denominator the same.

Using letters, this rule is written like this:
\(\large \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)

Multiplying fractions

To multiply a fraction by a fraction, you need to multiply their numerators and denominators and write the first product as the numerator, and the second as the denominator.

Using letters, the rule for multiplying fractions can be written as follows:
\(\large \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)

Using the formulated rule, you can multiply a fraction by a natural number, by a mixed fraction, and also multiply mixed fractions. To do this, you need to write a natural number as a fraction with a denominator of 1, a mixed fraction - as an improper fraction.

The result of multiplication should be simplified (if possible) by reducing the fraction and isolating the whole part of the improper fraction.

For fractions, as for natural numbers, the commutative and combinative properties of multiplication, as well as the distributive property of multiplication relative to addition, are valid.

Division of fractions

Let's take the fraction \(\frac(2)(3)\) and “flip” it, swapping the numerator and denominator. We get the fraction \(\frac(3)(2)\). This fraction is called reverse fractions \(\frac(2)(3)\).

If we now “reverse” the fraction \(\frac(3)(2)\), we will get the original fraction \(\frac(2)(3)\). Therefore, fractions such as \(\frac(2)(3)\) and \(\frac(3)(2)\) are called mutually inverse.

For example, the fractions \(\frac(6)(5) \) and \(\frac(5)(6) \), \(\frac(7)(18) \) and \(\frac (18)(7)\).

Using letters, reciprocal fractions can be written as follows: \(\frac(a)(b) \) and \(\frac(b)(a) \)

It is clear that the product of reciprocal fractions is equal to 1. For example: \(\frac(2)(3) \cdot \frac(3)(2) =1 \)

Using reciprocal fractions, you can reduce division of fractions to multiplication.

The rule for dividing a fraction by a fraction is:
To divide one fraction by another, you need to multiply the dividend by the reciprocal of the divisor.

Using letters, the rule for dividing fractions can be written as follows:
\(\large \frac(a)(b) : \frac(c)(d) = \frac(a)(b) \cdot \frac(d)(c) \)

If the dividend or divisor is a natural number or a mixed fraction, then in order to use the rule for dividing fractions, it must first be represented as an improper fraction.