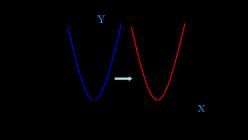
Graf funkciír = sekera 2 + n .

Vysvetlenie.

r = 2X 2 + 4.
r = 2X 2, posúva o štyri jednotky nahor r. Samozrejme, v tomto prípade všetky hodnoty r prirodzene zvýšiť o 4.

Tu je tabuľka funkčných hodnôt r = 2X 2:

X
r

A tu je tabuľka hodnôt r = 2X 2 + 4:

X
r

Z tabuľky vidíme, že vrchol paraboly druhej funkcie je o 4 jednotky vyšší ako vrchol prvej paraboly (jej súradnice sú 0;4). A hodnoty r druhá funkcia má ešte 4 hodnoty r prvá funkcia.

Graf funkciír = a(X – m) 2 .

Vysvetlenie.

Napríklad potrebujete nakresliť funkciu r = 2 (X – 6) 2 .
To znamená, že parabola, ktorá je grafom funkcie r = 2X 2, posúva o šesť jednotiek doprava pozdĺž osi X(na grafe - červená parabola).

Graf funkciír = a(X – m) 2 + n.

Tieto dve funkcie nás vedú k tretej funkcii: r = a(X – m) 2 + n.

Vysvetlenie:

Napríklad potrebujete nakresliť funkciu r = 2 (X – 6) 2 + 2.
To znamená, že parabola, ktorá je grafom funkcie r = 2X 2 sa posunie o 6 jednotiek doprava (hodnota m) a o 2 jednotky nahor (hodnota n). Červená parabola na grafe je výsledkom týchto pohybov.

1. Mocninná funkcia, jej vlastnosti a graf;

2. Transformácie:

Paralelný prenos;

Symetria okolo súradnicových osí;

Symetria o pôvode;

Symetria okolo priamky y = x;

Naťahovanie a zmršťovanie pozdĺž súradnicových osí.

3. Exponenciálna funkcia, jej vlastnosti a graf, podobné transformácie;

4. Logaritmická funkcia, jej vlastnosti a graf;

5. Goniometrická funkcia, jej vlastnosti a graf, podobné transformácie (y = sin x; y = cos x; y = tg x);

Funkcia: y = x\n - jej vlastnosti a graf.

Mocninná funkcia, jej vlastnosti a graf

y \u003d x, y \u003d x 2, y \u003d x 3, y \u003d 1 / x atď. Všetky tieto funkcie sú špeciálnymi prípadmi výkonovej funkcie, t.j. funkcie y = xp, kde p je dané reálne číslo.
Vlastnosti a graf mocninovej funkcie v podstate závisia od vlastností mocniny s reálnym exponentom a najmä od hodnôt, pre ktoré X A p dáva zmysel xp. Pristúpme k podobnej úvahe o rôznych prípadoch v závislosti od
exponent p.

1. Index p = 2n je párne prirodzené číslo.

y=x2n, Kde n je prirodzené číslo a má nasledujúce vlastnosti:

• definičný obor sú všetky reálne čísla, t.j. množina R;
• množina hodnôt - nezáporné čísla, t.j. y je väčšie alebo rovné 0;
• funkciu y=x2n dokonca, pretože x 2n = (-x) 2n
• funkcia na intervale klesá X< 0 a zvyšuje sa v intervale x > 0.

Graf funkcií y=x2n má rovnaký tvar ako napríklad graf funkcie y=x4.

2. Indikátor p = 2n - 1- nepárne prirodzené číslo

V tomto prípade funkcia napájania y=x2n-1, kde je prirodzené číslo, má tieto vlastnosti:

• doména definície - množina R;
• množina hodnôt - množina R;
• funkciu y=x2n-1 zvláštne, pretože (- x) 2n-1= x 2n-1;
• funkcia je rastúca na celej reálnej osi.

Graf funkcií y=x2n-1 y=x3.

3. Indikátor p = -2n, Kde n- prirodzené číslo.

V tomto prípade funkcia napájania y=x-2n=1/x2n má nasledujúce vlastnosti:

• množina hodnôt - kladné čísla y>0;
• funkcia y = 1/x2n dokonca, pretože 1/(-x) 2n= 1/x2n;
• funkcia je rastúca na intervale x0.

Graf funkcie y = 1/x2n má rovnaký tvar ako napríklad graf funkcie y = 1/x2.

4. Indikátor p = -(2n-1), Kde n- prirodzené číslo.
V tomto prípade funkcia napájania y=x-(2n-1) má nasledujúce vlastnosti:

• doménou definície je množina R, okrem x = 0;
• množina hodnôt - množina R, okrem y = 0;
• funkciu y=x-(2n-1) zvláštne, pretože (- x)-(2n-1) = -x-(2n-1);
• funkcia je v intervaloch klesajúca X< 0 A x > 0.

Graf funkcií y=x-(2n-1) má rovnaký tvar ako napríklad graf funkcie y = 1/x3.

Funkcia y \u003d x2n, kde n patrí do množiny kladných celých čísel. Mocninná funkcia tohto druhu má párny kladný exponent a=2n. Pretože vždy x2n=(-x)2n, grafy všetkých takýchto funkcií sú symetrické okolo osi y. Všetky funkcie tvaru y = x2n, n patriace do množiny kladných celých čísel majú tieto zhodné vlastnosti: X=R X? =(-?;?) Y=Vlastnosti funkcie arcsin

1. [Edit] Získanie funkcie arcsin

Daná funkcia v celom jeho domén náhodou je po častiach monotónne, a teda inverzná korešpondencia nie je funkcia. Preto berieme do úvahy interval, v ktorom sa striktne zvyšuje a nadobúda všetky hodnoty rozsahy- . Keďže pre funkciu na intervale každá hodnota argumentu zodpovedá jedinej hodnote funkcie, potom na tomto segmente existuje inverzná funkcia ktorého graf je symetrický ku grafu funkcie na úsečke vzhľadom na priamku

Na definičnom obore mocninnej funkcie y = x p platia tieto vzorce:
; ;
;
; ;
; ;
; .

Vlastnosti mocninných funkcií a ich grafy

Mocninná funkcia s exponentom rovným nule, p = 0

Ak je exponent mocninovej funkcie y = x p rovný nule, p = 0 , potom je mocninná funkcia definovaná pre všetky x ≠ 0 a je konštantná, rovná jednej:
y \u003d x p \u003d x 0 \u003d 1, x ≠ 0.

Mocninná funkcia s prirodzeným nepárnym exponentom, p = n = 1, 3, 5, ...

Uvažujme mocninnú funkciu y = x p = x n s prirodzeným nepárnym exponentom n = 1, 3, 5, ... . Takýto ukazovateľ možno zapísať aj ako: n = 2k + 1, kde k = 0, 1, 2, 3, ... je nezáporné celé číslo. Nižšie sú uvedené vlastnosti a grafy takýchto funkcií.

Graf mocninnej funkcie y = x n s prirodzeným nepárnym exponentom pre rôzne hodnoty exponentu n = 1, 3, 5, ... .

doména: -∞ < x < ∞
Viaceré hodnoty: -∞ < y < ∞
Parita: nepárne, y(-x) = - y(x)
Monotónne: zvyšuje monotónne
Extrémy: Nie
Konvexné:
pri -∞< x < 0 выпукла вверх
na 0< x < ∞ выпукла вниз
Body zlomu: x = 0, y = 0
x = 0, y = 0
Obmedzenia:
;
Súkromné ​​hodnoty:
pri x = -1,
y(-1) = (-1) n ≡ (-1) 2k+1 = -1
pre x = 0, y(0) = 0 n = 0
pre x = 1, y(1) = 1 n = 1
Obrátená funkcia:
pre n = 1 je funkcia inverzná k sebe samej: x = y
pre n ≠ 1 je inverzná funkcia koreňom stupňa n:

Mocninná funkcia s prirodzeným párnym exponentom, p = n = 2, 4, 6, ...

Uvažujme mocninnú funkciu y = x p = x n s prirodzeným párnym exponentom n = 2, 4, 6, ... . Takýto ukazovateľ možno zapísať aj ako: n = 2k, kde k = 1, 2, 3, ... je prirodzené číslo. Vlastnosti a grafy takýchto funkcií sú uvedené nižšie.

Graf mocninnej funkcie y = x n s prirodzeným párnym exponentom pre rôzne hodnoty exponentu n = 2, 4, 6, ... .

doména: -∞ < x < ∞
Viaceré hodnoty: 0 ≤ r< ∞
Parita: párne, y(-x) = y(x)
Monotónne:
pre x ≤ 0 monotónne klesá
pre x ≥ 0 monotónne rastie
Extrémy: minimum, x=0, y=0
Konvexné: konvexné nadol
Body zlomu: Nie
Priesečníky so súradnicovými osami: x = 0, y = 0
Obmedzenia:
;
Súkromné ​​hodnoty:
pre x = -1, y(-1) = (-1) n ≡ (-1) 2k = 1
pre x = 0, y(0) = 0 n = 0
pre x = 1, y(1) = 1 n = 1
Obrátená funkcia:
pre n = 2, druhá odmocnina:
pre n ≠ 2, koreň stupňa n:

Mocninná funkcia s celočíselným záporným exponentom, p = n = -1, -2, -3, ...

Uvažujme mocninnú funkciu y = x p = x n s exponentom celého záporného čísla n = -1, -2, -3, ... . Ak dáme n = -k, kde k = 1, 2, 3, ... je prirodzené číslo, môžeme ho znázorniť ako:

Graf mocninnej funkcie y = x n so záporným celočíselným exponentom pre rôzne hodnoty exponentu n = -1, -2, -3, ... .

Nepárny exponent, n = -1, -3, -5, ...

Nižšie sú uvedené vlastnosti funkcie y = x n s nepárnym záporným exponentom n = -1, -3, -5, ... .

doména: x ≠ 0
Viaceré hodnoty: y ≠ 0
Parita: nepárne, y(-x) = - y(x)
Monotónne: klesá monotónne
Extrémy: Nie
Konvexné:
pri x< 0 : выпукла вверх
pre x > 0 : konvexné nadol
Body zlomu: Nie
Priesečníky so súradnicovými osami: Nie
Znamenie:
pri x< 0, y < 0
pre x > 0, y > 0
Obmedzenia:
; ; ;
Súkromné ​​hodnoty:
pre x = 1, y(1) = 1 n = 1
Obrátená funkcia:
pre n = -1,
pre n< -2 ,

Párny exponent, n = -2, -4, -6, ...

Nižšie sú uvedené vlastnosti funkcie y = x n s párnym záporným exponentom n = -2, -4, -6, ... .

doména: x ≠ 0
Viaceré hodnoty: y > 0
Parita: párne, y(-x) = y(x)
Monotónne:
pri x< 0 : монотонно возрастает
pre x > 0 : monotónne klesajúci
Extrémy: Nie
Konvexné: konvexné nadol
Body zlomu: Nie
Priesečníky so súradnicovými osami: Nie
Znamenie: y > 0
Obmedzenia:
; ; ;
Súkromné ​​hodnoty:
pre x = 1, y(1) = 1 n = 1
Obrátená funkcia:
pre n = -2,
pre n< -2 ,

Mocninná funkcia s racionálnym (zlomkovým) exponentom

Uvažujme mocninnú funkciu y = x p s racionálnym (zlomkovým) exponentom , kde n je celé číslo, m > 1 je prirodzené číslo. Navyše n, m nemajú spoločných deliteľov.

Menovateľ zlomkového ukazovateľa je nepárny

Nech je menovateľ zlomkového exponentu nepárny: m = 3, 5, 7, ... . V tomto prípade je výkonová funkcia x p definovaná pre kladné aj záporné hodnoty x. Zvážte vlastnosti takýchto mocninných funkcií, keď je exponent p v určitých medziach.

p je záporné, p< 0

Nech je racionálny exponent (s nepárnym menovateľom m = 3, 5, 7, ... ) menší ako nula: .

Grafy exponenciálnych funkcií s racionálnym záporným exponentom pre rôzne hodnoty exponentu, kde m = 3, 5, 7, ... je nepárne.

Nepárny čitateľ, n = -1, -3, -5, ...

Tu sú vlastnosti mocninovej funkcie y = x p s racionálnym záporným exponentom , kde n = -1, -3, -5, ... je nepárne záporné celé číslo, m = 3, 5, 7 ... je nepárne prirodzené číslo.

doména: x ≠ 0
Viaceré hodnoty: y ≠ 0
Parita: nepárne, y(-x) = - y(x)
Monotónne: klesá monotónne
Extrémy: Nie
Konvexné:
pri x< 0 : выпукла вверх
pre x > 0 : konvexné nadol
Body zlomu: Nie
Priesečníky so súradnicovými osami: Nie
Znamenie:
pri x< 0, y < 0
pre x > 0, y > 0
Obmedzenia:
; ; ;
Súkromné ​​hodnoty:
pre x = -1, y(-1) = (-1) n = -1
pre x = 1, y(1) = 1 n = 1
Obrátená funkcia:

Párny čitateľ, n = -2, -4, -6, ...

Vlastnosti mocninovej funkcie y = x p s racionálnym záporným exponentom, kde n = -2, -4, -6, ... je párne záporné celé číslo, m = 3, 5, 7 ... je nepárne prirodzené číslo .

doména: x ≠ 0
Viaceré hodnoty: y > 0
Parita: párne, y(-x) = y(x)
Monotónne:
pri x< 0 : монотонно возрастает
pre x > 0 : monotónne klesajúci
Extrémy: Nie
Konvexné: konvexné nadol
Body zlomu: Nie
Priesečníky so súradnicovými osami: Nie
Znamenie: y > 0
Obmedzenia:
; ; ;
Súkromné ​​hodnoty:
pre x = -1, y(-1) = (-1) n = 1
pre x = 1, y(1) = 1 n = 1
Obrátená funkcia:

Hodnota p je kladná, menšia ako jedna, 0< p < 1

Graf mocninovej funkcie s racionálnym exponentom (0< p < 1 ) при различных значениях показателя степени , где m = 3, 5, 7, ... - нечетное.

Nepárny čitateľ, n = 1, 3, 5, ...

< p < 1 , где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

doména: -∞ < x < +∞
Viaceré hodnoty: -∞ < y < +∞
Parita: nepárne, y(-x) = - y(x)
Monotónne: zvyšuje monotónne
Extrémy: Nie
Konvexné:
pri x< 0 : выпукла вниз
pre x > 0 : konvexné nahor
Body zlomu: x = 0, y = 0
Priesečníky so súradnicovými osami: x = 0, y = 0
Znamenie:
pri x< 0, y < 0
pre x > 0, y > 0
Obmedzenia:
;
Súkromné ​​hodnoty:
pre x = -1, y(-1) = -1
pre x = 0, y(0) = 0
pre x = 1, y(1) = 1
Obrátená funkcia:

Párny čitateľ, n = 2, 4, 6, ...

Prezentované sú vlastnosti mocninnej funkcie y = x p s racionálnym exponentom , ktorý je v rámci 0.< p < 1 , где n = 2, 4, 6, ... - четное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

doména: -∞ < x < +∞
Viaceré hodnoty: 0 ≤ r< +∞
Parita: párne, y(-x) = y(x)
Monotónne:
pri x< 0 : монотонно убывает
pre x > 0 : monotónne rastúce
Extrémy: minimum pri x = 0, y = 0
Konvexné: konvexné smerom nahor pri x ≠ 0
Body zlomu: Nie
Priesečníky so súradnicovými osami: x = 0, y = 0
Znamenie: pre x ≠ 0, y > 0
Obmedzenia:
;
Súkromné ​​hodnoty:
pre x = -1, y(-1) = 1
pre x = 0, y(0) = 0
pre x = 1, y(1) = 1
Obrátená funkcia:

Exponent p je väčší ako jedna, p > 1

Graf mocninnej funkcie s racionálnym exponentom (p > 1 ) pre rôzne hodnoty exponentu, kde m = 3, 5, 7, ... je nepárne.

Nepárny čitateľ, n = 5, 7, 9, ...

Vlastnosti mocninnej funkcie y = x p s racionálnym exponentom väčším ako jedna: . Kde n = 5, 7, 9, ... je nepárne prirodzené číslo, m = 3, 5, 7 ... je nepárne prirodzené číslo.

doména: -∞ < x < ∞
Viaceré hodnoty: -∞ < y < ∞
Parita: nepárne, y(-x) = - y(x)
Monotónne: zvyšuje monotónne
Extrémy: Nie
Konvexné:
pri -∞< x < 0 выпукла вверх
na 0< x < ∞ выпукла вниз
Body zlomu: x = 0, y = 0
Priesečníky so súradnicovými osami: x = 0, y = 0
Obmedzenia:
;
Súkromné ​​hodnoty:
pre x = -1, y(-1) = -1
pre x = 0, y(0) = 0
pre x = 1, y(1) = 1
Obrátená funkcia:

Párny čitateľ, n = 4, 6, 8, ...

Vlastnosti mocninnej funkcie y = x p s racionálnym exponentom väčším ako jedna: . Kde n = 4, 6, 8, ... je párne prirodzené číslo, m = 3, 5, 7 ... je nepárne prirodzené číslo.

doména: -∞ < x < ∞
Viaceré hodnoty: 0 ≤ r< ∞
Parita: párne, y(-x) = y(x)
Monotónne:
pri x< 0 монотонно убывает
pre x > 0 monotónne rastie
Extrémy: minimum pri x = 0, y = 0
Konvexné: konvexné nadol
Body zlomu: Nie
Priesečníky so súradnicovými osami: x = 0, y = 0
Obmedzenia:
;
Súkromné ​​hodnoty:
pre x = -1, y(-1) = 1
pre x = 0, y(0) = 0
pre x = 1, y(1) = 1
Obrátená funkcia:

Menovateľ zlomkového ukazovateľa je párny

Nech je menovateľ zlomkového exponentu párny: m = 2, 4, 6, ... . V tomto prípade mocninná funkcia x p nie je definovaná pre záporné hodnoty argumentu. Jeho vlastnosti sa zhodujú s vlastnosťami mocninnej funkcie s iracionálnym exponentom (pozri nasledujúcu časť).

Mocninná funkcia s iracionálnym exponentom

Uvažujme mocninnú funkciu y = x p s iracionálnym exponentom p . Vlastnosti takýchto funkcií sa líšia od vlastností uvedených vyššie v tom, že nie sú definované pre záporné hodnoty argumentu x. Pre kladné hodnoty argumentu závisia vlastnosti iba od hodnoty exponentu p a nezávisia od toho, či je p celé číslo, racionálne alebo iracionálne.

y = x p pre rôzne hodnoty exponentu p .

Mocninná funkcia so zápornou p< 0

doména: x > 0
Viaceré hodnoty: y > 0
Monotónne: klesá monotónne
Konvexné: konvexné nadol
Body zlomu: Nie
Priesečníky so súradnicovými osami: Nie
Obmedzenia: ;
súkromná hodnota: Pre x = 1, y(1) = 1 p = 1

Mocninná funkcia s kladným exponentom p > 0

Indikátor je menší ako jedna 0< p < 1

doména: x ≥ 0
Viaceré hodnoty: y ≥ 0
Monotónne: zvyšuje monotónne
Konvexné: konvexne nahor
Body zlomu: Nie
Priesečníky so súradnicovými osami: x = 0, y = 0
Obmedzenia:
Súkromné ​​hodnoty: Pre x = 0, y(0) = 0 p = 0.
Pre x = 1, y(1) = 1 p = 1

Indikátor je väčší ako jedno p > 1

doména: x ≥ 0
Viaceré hodnoty: y ≥ 0
Monotónne: zvyšuje monotónne
Konvexné: konvexné nadol
Body zlomu: Nie
Priesečníky so súradnicovými osami: x = 0, y = 0
Obmedzenia:
Súkromné ​​hodnoty: Pre x = 0, y(0) = 0 p = 0.
Pre x = 1, y(1) = 1 p = 1

Referencie:
I.N. Bronstein, K.A. Semendyaev, Príručka matematiky pre inžinierov a študentov vysokých škôl, Lan, 2009.