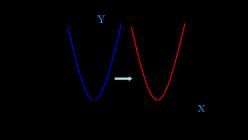
Graph einer Funktionj = Axt 2 + N .

Erläuterung.

j = 2X 2 + 4.
j = 2X 2, bewegt sich um vier Einheiten entlang der Achse nach oben j. Natürlich alle Bedeutungen j natürlich um 4 erhöhen.

Hier ist eine Tabelle mit Funktionswerten j = 2X 2:

X
j

Und hier ist eine Wertetabelle j = 2X 2 + 4:

X
j

Aus der Tabelle sehen wir, dass der Scheitelpunkt der Parabel der zweiten Funktion 4 Einheiten höher ist als der Scheitelpunkt der ersten Parabel (ihre Koordinaten sind 0;4). Und die Bedeutungen j Die zweite Funktion hat 4 weitere Werte j erste Funktion.

Graph einer Funktionj = A(X – M) 2 .

Erläuterung.

Beispielsweise müssen Sie eine Funktion grafisch darstellen j = 2 (X – 6) 2 .
Dies bedeutet, dass die Parabel der Graph der Funktion ist j = 2X 2, bewegt sich entlang der Achse um sechs Einheiten nach rechts X(Auf der Grafik ist eine rote Parabel zu sehen.)

Graph einer Funktionj = A(X – M) 2 + N.

Zwei Funktionen führen uns zur dritten Funktion: j = A(X – M) 2 + N.

Erläuterung:

Beispielsweise müssen Sie eine Funktion grafisch darstellen j = 2 (X – 6) 2 + 2.
Dies bedeutet, dass die Parabel der Graph der Funktion ist j = 2X 2 , bewegt sich um 6 Einheiten nach rechts (der Wert von m) und 2 Einheiten nach oben (der Wert von n). Die rote Parabel im Diagramm ist das Ergebnis dieser Bewegungen.

1. Potenzfunktion, ihre Eigenschaften und Graph;

2. Transformationen:

Parallelübertragung;

Symmetrie um Koordinatenachsen;

Symmetrie über den Ursprung;

Symmetrie um die Gerade y = x;

Dehnung und Stauchung entlang der Koordinatenachsen.

3. Exponentialfunktion, ihre Eigenschaften und Graph, ähnliche Transformationen;

4. Logarithmische Funktion, ihre Eigenschaften und ihr Diagramm;

5. Trigonometrische Funktion, ihre Eigenschaften und Graph, ähnliche Transformationen (y = sin x; y = cos x; y = tan x);

Funktion: y = x\n – seine Eigenschaften und sein Diagramm.

Potenzfunktion, ihre Eigenschaften und Graph

y = x, y = x 2, y = x 3, y = 1/x usw. Alle diese Funktionen sind Spezialfälle der Potenzfunktion, also der Funktion y = x p, wobei p eine gegebene reelle Zahl ist.
Die Eigenschaften und der Graph einer Potenzfunktion hängen maßgeblich von den Eigenschaften einer Potenz mit reellem Exponenten und insbesondere von deren Werten ab X Und P Abschluss macht Sinn xp. Fahren wir mit einer ähnlichen Betrachtung verschiedener Fälle fort, je nachdem
Exponent P.

1. Index p = 2n- eine gerade natürliche Zahl.

y = x2n, Wo N- eine natürliche Zahl, hat folgende Eigenschaften:

• Definitionsbereich – alle reellen Zahlen, also die Menge R;
• Wertemenge – nicht negative Zahlen, d. h. y ist größer oder gleich 0;
• Funktion y = x2n sogar, weil x 2n = (-x) 2n
• Die Funktion nimmt im Intervall ab X< 0 und im Intervall zunehmend x > 0.

Graph einer Funktion y = x2n hat die gleiche Form wie beispielsweise der Graph einer Funktion y = x 4.

2. Indikator p = 2n - 1- ungerade natürliche Zahl

In diesem Fall die Potenzfunktion y = x2n-1, wobei es sich um eine natürliche Zahl handelt, hat die folgenden Eigenschaften:

• Definitionsbereich - Menge R;
• Wertemenge - Menge R;
• Funktion y = x2n-1 seltsam, weil (- x) 2n-1= x2n-1;
• die Funktion nimmt auf der gesamten reellen Achse zu.

Graph einer Funktion y = x2n-1 y = x 3.

3. Indikator p = -2n, Wo N- natürliche Zahl.

In diesem Fall die Potenzfunktion y = x -2n = 1/x 2n hat die folgenden Eigenschaften:

• Wertemenge – positive Zahlen y>0;
• Funktion y = 1/x2n sogar, weil 1/(-x)2n= 1/x 2n;
• Die Funktion wächst im Intervall x0.

Graph der Funktion y = 1/x2n hat die gleiche Form wie beispielsweise der Graph der Funktion y = 1/x 2.

4. Indikator p = -(2n-1), Wo N- natürliche Zahl.
In diesem Fall die Potenzfunktion y = x -(2n-1) hat die folgenden Eigenschaften:

• Definitionsbereich - Menge R, außer x = 0;
• Wertemenge – Menge R, außer y = 0;
• Funktion y = x -(2n-1) seltsam, weil (- x) -(2n-1) = -x -(2n-1);
• Die Funktion nimmt in Intervallen ab X< 0 Und x > 0.

Graph einer Funktion y = x -(2n-1) hat die gleiche Form wie beispielsweise der Graph einer Funktion y = 1/x 3.

Funktion y = x2n, wobei n zur Menge der positiven ganzen Zahlen gehört. Eine solche Potenzfunktion hat einen geraden positiven Exponenten a=2n. Da x2n = (-x)2n immer ist, sind die Graphen aller dieser Funktionen symmetrisch zur Ordinate. Alle Funktionen der Form y = x2n, n gehören zur Menge der positiven ganzen Zahlen und haben die folgenden identischen Eigenschaften: X = R X? =(-?;?) У=Eigenschaften der arcsin-Funktion

1. [Bearbeiten]Die Arcsin-Funktion abrufen

Angesichts der Funktion im gesamten Definitionsbereich das ist sie zufällig stückweise monoton und daher die umgekehrte Entsprechung ist keine Funktion. Daher betrachten wir das Segment, in dem es streng ansteigt und alle Werte annimmt Wertebereich- . Da für eine Funktion in einem Intervall jeder Wert des Arguments einem einzelnen Wert der Funktion entspricht, ist dies in diesem Intervall der Fall Umkehrfunktion dessen Graph symmetrisch zum Graphen einer Funktion auf einer Strecke relativ zu einer Geraden ist

Im Definitionsbereich der Potenzfunktion y = x p gelten folgende Formeln:
; ;
;
; ;
; ;
; .

Eigenschaften von Potenzfunktionen und ihren Graphen

Potenzfunktion mit Exponent gleich Null, p = 0

Wenn der Exponent der Potenzfunktion y = x p gleich Null ist, p = 0, dann ist die Potenzfunktion für alle x ≠ 0 definiert und eine Konstante gleich eins:
y = x p = x 0 = 1, x ≠ 0.

Potenzfunktion mit natürlichem ungeraden Exponenten, p = n = 1, 3, 5, ...

Betrachten Sie eine Potenzfunktion y = x p = x n mit einem natürlichen ungeraden Exponenten n = 1, 3, 5, ... . Dieser Indikator kann auch in der Form geschrieben werden: n = 2k + 1, wobei k = 0, 1, 2, 3, ... eine nicht negative ganze Zahl ist. Nachfolgend finden Sie die Eigenschaften und Diagramme solcher Funktionen.

Graph einer Potenzfunktion y = x n mit einem natürlichen ungeraden Exponenten für verschiedene Werte des Exponenten n = 1, 3, 5, ....

Domain: -∞ < x < ∞
Mehrere Bedeutungen: -∞ < y < ∞
Parität: ungerade, y(-x) = - y(x)
Monoton: monoton zunimmt
Extreme: Nein
Konvex:
bei -∞< x < 0 выпукла вверх
bei 0< x < ∞ выпукла вниз
Wendepunkte: x = 0, y = 0
x = 0, y = 0
Grenzen:
;
Private Werte:
bei x = -1,
y(-1) = (-1) n ≡ (-1) 2k+1 = -1
bei x = 0, y(0) = 0 n = 0
für x = 1, y(1) = 1 n = 1
Umkehrfunktion:
Für n = 1 ist die Funktion ihre Umkehrung: x = y
für n ≠ 1 ist die Umkehrfunktion die Wurzel vom Grad n:

Potenzfunktion mit natürlichem geradem Exponenten, p = n = 2, 4, 6, ...

Betrachten Sie eine Potenzfunktion y = x p = x n mit einem natürlichen geraden Exponenten n = 2, 4, 6, .... Dieser Indikator kann auch in der Form geschrieben werden: n = 2k, wobei k = 1, 2, 3, ... - natürlich. Die Eigenschaften und Diagramme solcher Funktionen sind unten angegeben.

Graph einer Potenzfunktion y = x n mit einem natürlichen geraden Exponenten für verschiedene Werte des Exponenten n = 2, 4, 6, ....

Domain: -∞ < x < ∞
Mehrere Bedeutungen: 0 ≤ y< ∞
Parität: gerade, y(-x) = y(x)
Monoton:
für x ≤ 0 nimmt es monoton ab
für x ≥ 0 nimmt monoton zu
Extreme: Minimum, x = 0, y = 0
Konvex: konvex nach unten
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: x = 0, y = 0
Grenzen:
;
Private Werte:
bei x = -1, y(-1) = (-1) n ≡ (-1) 2k = 1
bei x = 0, y(0) = 0 n = 0
für x = 1, y(1) = 1 n = 1
Umkehrfunktion:
für n = 2, Quadratwurzel:
für n ≠ 2, Wurzel vom Grad n:

Potenzfunktion mit negativem ganzzahligem Exponenten, p = n = -1, -2, -3, ...

Betrachten Sie eine Potenzfunktion y = x p = x n mit einem ganzzahligen negativen Exponenten n = -1, -2, -3, .... Wenn wir n = -k setzen, wobei k = 1, 2, 3, ... eine natürliche Zahl ist, dann kann sie wie folgt dargestellt werden:

Graph einer Potenzfunktion y = x n mit einem negativen ganzzahligen Exponenten für verschiedene Werte des Exponenten n = -1, -2, -3, ... .

Ungerader Exponent, n = -1, -3, -5, ...

Nachfolgend sind die Eigenschaften der Funktion y = x n mit einem ungeraden negativen Exponenten n = -1, -3, -5, ... aufgeführt.

Domain: x ≠ 0
Mehrere Bedeutungen: y ≠ 0
Parität: ungerade, y(-x) = - y(x)
Monoton: nimmt monoton ab
Extreme: Nein
Konvex:
bei x< 0 : выпукла вверх
für x > 0: konvex nach unten
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: Nein
Zeichen:
bei x< 0, y < 0
für x > 0, y > 0
Grenzen:
; ; ;
Private Werte:
für x = 1, y(1) = 1 n = 1
Umkehrfunktion:
wenn n = -1,
bei n< -2 ,

Gerader Exponent, n = -2, -4, -6, ...

Nachfolgend sind die Eigenschaften der Funktion y = x n mit einem geraden negativen Exponenten n = -2, -4, -6, ... aufgeführt.

Domain: x ≠ 0
Mehrere Bedeutungen: y > 0
Parität: gerade, y(-x) = y(x)
Monoton:
bei x< 0 : монотонно возрастает
für x > 0: monoton abnehmend
Extreme: Nein
Konvex: konvex nach unten
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: Nein
Zeichen: y > 0
Grenzen:
; ; ;
Private Werte:
für x = 1, y(1) = 1 n = 1
Umkehrfunktion:
bei n = -2,
bei n< -2 ,

Potenzfunktion mit rationalem (gebrochenem) Exponenten

Betrachten Sie eine Potenzfunktion y = x p mit einem rationalen (gebrochenen) Exponenten, wobei n eine ganze Zahl und m > 1 eine natürliche Zahl ist. Darüber hinaus haben n, m keine gemeinsamen Teiler.

Der Nenner des Bruchindikators ist ungerade

Der Nenner des gebrochenen Exponenten sei ungerade: m = 3, 5, 7, ... . In diesem Fall ist die Potenzfunktion x p sowohl für positive als auch für negative Werte des Arguments x definiert. Betrachten wir die Eigenschaften solcher Potenzfunktionen, wenn der Exponent p innerhalb bestimmter Grenzen liegt.

Der p-Wert ist negativ, p< 0

Der rationale Exponent (mit ungeradem Nenner m = 3, 5, 7, ...) sei kleiner als Null: .

Diagramme von Potenzfunktionen mit einem rationalen negativen Exponenten für verschiedene Werte des Exponenten, wobei m = 3, 5, 7, ... – ungerade.

Ungerader Zähler, n = -1, -3, -5, ...

Wir stellen die Eigenschaften der Potenzfunktion y = x p mit einem rationalen negativen Exponenten dar, wobei n = -1, -3, -5, ... eine ungerade negative ganze Zahl ist, m = 3, 5, 7 ... eine ungerade natürliche ganze Zahl.

Domain: x ≠ 0
Mehrere Bedeutungen: y ≠ 0
Parität: ungerade, y(-x) = - y(x)
Monoton: nimmt monoton ab
Extreme: Nein
Konvex:
bei x< 0 : выпукла вверх
für x > 0: konvex nach unten
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: Nein
Zeichen:
bei x< 0, y < 0
für x > 0, y > 0
Grenzen:
; ; ;
Private Werte:
bei x = -1, y(-1) = (-1) n = -1
für x = 1, y(1) = 1 n = 1
Umkehrfunktion:

Gerader Zähler, n = -2, -4, -6, ...

Eigenschaften der Potenzfunktion y = x p mit einem rationalen negativen Exponenten, wobei n = -2, -4, -6, ... eine gerade negative ganze Zahl ist, m = 3, 5, 7 ... eine ungerade natürliche ganze Zahl ist .

Domain: x ≠ 0
Mehrere Bedeutungen: y > 0
Parität: gerade, y(-x) = y(x)
Monoton:
bei x< 0 : монотонно возрастает
für x > 0: monoton abnehmend
Extreme: Nein
Konvex: konvex nach unten
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: Nein
Zeichen: y > 0
Grenzen:
; ; ;
Private Werte:
bei x = -1, y(-1) = (-1) n = 1
für x = 1, y(1) = 1 n = 1
Umkehrfunktion:

Der p-Wert ist positiv, kleiner als eins, 0< p < 1

Graph einer Potenzfunktion mit rationalem Exponenten (0< p < 1 ) при различных значениях показателя степени , где m = 3, 5, 7, ... - нечетное.

Ungerader Zähler, n = 1, 3, 5, ...

< p < 1 , где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Domain: -∞ < x < +∞
Mehrere Bedeutungen: -∞ < y < +∞
Parität: ungerade, y(-x) = - y(x)
Monoton: monoton zunimmt
Extreme: Nein
Konvex:
bei x< 0 : выпукла вниз
für x > 0: konvex nach oben
Wendepunkte: x = 0, y = 0
Schnittpunkte mit Koordinatenachsen: x = 0, y = 0
Zeichen:
bei x< 0, y < 0
für x > 0, y > 0
Grenzen:
;
Private Werte:
bei x = -1, y(-1) = -1
bei x = 0, y(0) = 0
für x = 1, y(1) = 1
Umkehrfunktion:

Gerader Zähler, n = 2, 4, 6, ...

Die Eigenschaften der Potenzfunktion y = x p mit einem rationalen Exponenten innerhalb von 0 werden vorgestellt< p < 1 , где n = 2, 4, 6, ... - четное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Domain: -∞ < x < +∞
Mehrere Bedeutungen: 0 ≤ y< +∞
Parität: gerade, y(-x) = y(x)
Monoton:
bei x< 0 : монотонно убывает
für x > 0: monoton steigend
Extreme: Minimum bei x = 0, y = 0
Konvex: konvex nach oben für x ≠ 0
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: x = 0, y = 0
Zeichen: für x ≠ 0, y > 0
Grenzen:
;
Private Werte:
bei x = -1, y(-1) = 1
bei x = 0, y(0) = 0
für x = 1, y(1) = 1
Umkehrfunktion:

Der p-Index ist größer als eins, p > 1

Diagramm einer Potenzfunktion mit einem rationalen Exponenten (p > 1) für verschiedene Werte des Exponenten, wobei m = 3, 5, 7, ... – ungerade.

Ungerader Zähler, n = 5, 7, 9, ...

Eigenschaften der Potenzfunktion y = x p mit einem rationalen Exponenten größer als eins: . Wobei n = 5, 7, 9, ... – ungerade natürlich, m = 3, 5, 7 ... – ungerade natürlich.

Domain: -∞ < x < ∞
Mehrere Bedeutungen: -∞ < y < ∞
Parität: ungerade, y(-x) = - y(x)
Monoton: monoton zunimmt
Extreme: Nein
Konvex:
bei -∞< x < 0 выпукла вверх
bei 0< x < ∞ выпукла вниз
Wendepunkte: x = 0, y = 0
Schnittpunkte mit Koordinatenachsen: x = 0, y = 0
Grenzen:
;
Private Werte:
bei x = -1, y(-1) = -1
bei x = 0, y(0) = 0
für x = 1, y(1) = 1
Umkehrfunktion:

Gerader Zähler, n = 4, 6, 8, ...

Eigenschaften der Potenzfunktion y = x p mit einem rationalen Exponenten größer als eins: . Wobei n = 4, 6, 8, ... - gerade natürlich, m = 3, 5, 7 ... - ungerade natürlich.

Domain: -∞ < x < ∞
Mehrere Bedeutungen: 0 ≤ y< ∞
Parität: gerade, y(-x) = y(x)
Monoton:
bei x< 0 монотонно убывает
für x > 0 steigt monoton
Extreme: Minimum bei x = 0, y = 0
Konvex: konvex nach unten
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: x = 0, y = 0
Grenzen:
;
Private Werte:
bei x = -1, y(-1) = 1
bei x = 0, y(0) = 0
für x = 1, y(1) = 1
Umkehrfunktion:

Der Nenner des Bruchindikators ist gerade

Der Nenner des gebrochenen Exponenten sei gerade: m = 2, 4, 6, ... . In diesem Fall ist die Potenzfunktion x p für negative Werte des Arguments nicht definiert. Seine Eigenschaften stimmen mit den Eigenschaften einer Potenzfunktion mit irrationalem Exponenten überein (siehe nächster Abschnitt).

Potenzfunktion mit irrationalem Exponenten

Betrachten Sie eine Potenzfunktion y = x p mit einem irrationalen Exponenten p. Die Eigenschaften solcher Funktionen unterscheiden sich von den oben diskutierten darin, dass sie nicht für negative Werte des Arguments x definiert sind. Bei positiven Werten des Arguments hängen die Eigenschaften nur vom Wert des Exponenten p ab und nicht davon, ob p ganzzahlig, rational oder irrational ist.

y = x p für verschiedene Werte des Exponenten p.

Potenzfunktion mit negativem Exponenten p< 0

Domain: x > 0
Mehrere Bedeutungen: y > 0
Monoton: nimmt monoton ab
Konvex: konvex nach unten
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: Nein
Grenzen: ;
Private Bedeutung: Für x = 1, y(1) = 1 p = 1

Potenzfunktion mit positivem Exponenten p > 0

Indikator kleiner als eins 0< p < 1

Domain: x ≥ 0
Mehrere Bedeutungen: y ≥ 0
Monoton: monoton zunimmt
Konvex: konvex nach oben
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: x = 0, y = 0
Grenzen:
Private Werte: Für x = 0, y(0) = 0 p = 0 .
Für x = 1, y(1) = 1 p = 1

Der Indikator ist größer als eins p > 1

Domain: x ≥ 0
Mehrere Bedeutungen: y ≥ 0
Monoton: monoton zunimmt
Konvex: konvex nach unten
Wendepunkte: Nein
Schnittpunkte mit Koordinatenachsen: x = 0, y = 0
Grenzen:
Private Werte: Für x = 0, y(0) = 0 p = 0 .
Für x = 1, y(1) = 1 p = 1

Verweise:
IN. Bronstein, K.A. Semendyaev, Handbuch der Mathematik für Ingenieure und Studenten, „Lan“, 2009.