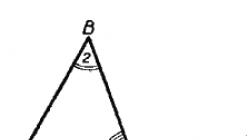
Veta o súčte uhlov trojuholníka. Súčet uhlov trojuholníka. Veta o súčte uhlov trojuholníka Prečo je súčet uhlov trojuholníka 180

Veta. Súčet vnútorných uhlov trojuholníka sa rovná dvom pravým uhlom.

Zoberme si trojuholník ABC (obr. 208). Označme jej vnútorné uhly číslami 1, 2 a 3. Dokážme to

∠1 + ∠2 + ∠3 = 180°.

Nakreslime cez nejaký vrchol trojuholníka, napríklad B, priamku MN rovnobežnú s AC.

Vo vrchole B sme dostali tri uhly: ∠4, ∠2 a ∠5. Ich súčet je priamy uhol, preto sa rovná 180°:

∠4 + ∠2 + ∠5 = 180°.

Ale ∠4 = ∠1 sú vnútorné priečne uhly s rovnobežkami MN a AC a sečnicou AB.

∠5 = ∠3 - ide o vnútorné priečne uhly s rovnobežkami MN a AC a sečnicou BC.

To znamená, že ∠4 a ∠5 možno nahradiť ich rovnými ∠1 a ∠3.

Preto ∠1 + ∠2 + ∠3 = 180°. Veta bola dokázaná.

2. Vlastnosť vonkajšieho uhla trojuholníka.

Veta. Vonkajší uhol trojuholníka sa rovná súčtu dvoch vnútorných uhlov, ktoré s ním nesusedia.

V skutočnosti v trojuholníku ABC (obr. 209) ∠1 + ∠2 = 180° - ∠3, ale aj ∠ВСD je vonkajší uhol tohto trojuholníka, ktorý nesusedí s ∠1 a ∠2, tiež rovný 180°. - ∠3 .

Takto:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Preto ∠1 + ∠2= ∠BCD.

Odvodená vlastnosť vonkajšieho uhla trojuholníka objasňuje obsah predtým dokázanej vety o vonkajšom uhle trojuholníka, ktorá uvádzala len to, že vonkajší uhol trojuholníka je väčší ako každý vnútorný uhol trojuholníka, ktorý s ním nesusedí; teraz sa zistilo, že vonkajší uhol sa rovná súčtu oboch vnútorných uhlov, ktoré s ním nesusedia.

3. Vlastnosť pravouhlého trojuholníka s uhlom 30°.

Veta. Rameno pravouhlého trojuholníka ležiace oproti uhlu 30° sa rovná polovici prepony.

Nech je uhol B v pravouhlom trojuholníku ACB rovný 30° (obr. 210). Potom bude jeho ďalší ostrý uhol rovný 60°.

Dokážme, že úsek AC sa rovná polovici prepony AB. Predĺžme nohu AC za vrchol pravého uhla C a odložme úsečku CM rovnajúcu sa úsečke AC. Spojme bod M s bodom B. Výsledný trojuholník ВСМ sa rovná trojuholníku ACB. Vidíme, že každý uhol trojuholníka ABM je rovný 60°, preto je tento trojuholník rovnostranný.

Úsek AC sa rovná polovici AM a keďže AM sa rovná AB, úsek AC sa bude rovnať polovici prepony AB.

Dokážete, že súčet uhlov v trojuholníku sa rovná 180 stupňom? a dostal najlepšiu odpoveď

Odpoveď od Top_ed[guru]
Načo dokazovať niečo, čo je už veľmi, veľmi dávno dokázané.
Veta o sume trojuholníka, klasická veta euklidovskej geometrie, to tvrdí
Súčet uhlov trojuholníka je 180°.
Nech ABC je ľubovoľný trojuholník. Nakreslite čiaru cez vrchol B rovnobežnú s čiarou AC. Označme na ňom bod D tak, aby body A a D ležali na opačných stranách priamky BC.
Uhly DBC a ACB sú zhodné ako vnútorné priečne ležiace uhly tvorené priečnym BC s rovnobežnými čiarami AC a BD. Preto sa súčet uhlov trojuholníka vo vrcholoch B a C rovná uhlu ABD.
Súčet všetkých troch uhlov trojuholníka sa rovná súčtu uhlov ABD a BAC. Keďže ide o jednostranné vnútorné uhly pre paralelné AC a BD a sečnicu AB, ich súčet je 180°. Veta bola dokázaná.

Odpoveď od Boriska(c)[guru]
Môžem, ale nepamätám si ako))

Odpoveď od Murashkina[guru]
Môcť. Je to pre vás naliehavé? ? Robíš skúšku z piatej triedy? ? :))

Odpoveď od Oriy Semykin[guru]
1. Záleží na geometrii priestoru. Na Riemannovej rovine > 180, na námestí. Lobačevského< 180. На Эвклидовой - равенство.
2. Nakreslite čiaru cez vrchol rovnobežnú s jednou zo strán a preskúmajte priečne uhly, ktoré tvoria dve strany a ďalšia čiara. Výsledný uhol (180) sa rovná súčtu troch uhlov trojuholníka.

Dôkaz sa v podstate opiera o skutočnosť, že je možné nakresliť iba jednu rovnobežnú čiaru. Existuje veľa geometrií, kde to tak nie je.

Odpoveď od Yuri[guru]
Prečo dokazovať to, čo sa osvedčilo?)) Ak chcete niečo nové, rozrežte štvorec na dve časti))

Odpoveď od Nikolaj Evgenievič[guru]
Nemôžem.

Odpoveď od Alex Brichka[expert]
Áno, tu nie je čo dokazovať, stačí k sebe pridať uhly a je to.

Odpoveď od 2 odpovede[guru]

Ahoj! Tu je výber tém s odpoveďami na vašu otázku: Dokážete, že súčet uhlov v trojuholníku sa rovná 180 stupňom?

Predbežná informácia

Najprv sa pozrime priamo na koncept trojuholníka.

Definícia 1

Trojuholník nazveme geometrický útvar, ktorý tvoria tri body navzájom spojené úsečkami (obr. 1).

Definícia 2

V rámci Definície 1 budeme body nazývať vrcholy trojuholníka.

Definícia 3

V rámci definície 1 sa segmenty budú nazývať strany trojuholníka.

Je zrejmé, že každý trojuholník bude mať 3 vrcholy a tri strany.

Veta o súčte uhlov v trojuholníku

Zaveďme a dokážme jednu z hlavných teorém súvisiacich s trojuholníkmi, a to vetu o súčte uhlov v trojuholníku.

Veta 1

Súčet uhlov v ľubovoľnom trojuholníku je $180^\circ$.

Dôkaz.

Zoberme si trojuholník $EGF$. Dokážme, že súčet uhlov v tomto trojuholníku sa rovná $180^\circ$. Urobme dodatočnú konštrukciu: nakreslite priamku $XY||EG$ (obr. 2)

Keďže priamky $XY$ a $EG$ sú rovnobežné, potom $∠E=∠XFE$ ležia priečne na sečne $FE$ a $∠G=∠YFG$ ležia priečne na sečne $FG$

Uhol $XFY$ bude obrátený, a preto sa rovná $180^\circ$.

$∠XFY=∠XFE+∠F+∠YFG=180^\circ$

Preto

$∠E+∠F+∠G=180^\circ$

Veta bola dokázaná.

Veta o vonkajšom uhle trojuholníka

Ďalšia veta o súčte uhlov pre trojuholník môže byť považovaná za vetu o vonkajšom uhle. Najprv si predstavme tento pojem.

Definícia 4

Vonkajším uhlom trojuholníka budeme nazývať uhol, ktorý bude susediť s ľubovoľným uhlom trojuholníka (obr. 3).

Uvažujme teraz teorém priamo.

Veta 2

Vonkajší uhol trojuholníka sa rovná súčtu dvoch uhlov trojuholníka, ktoré s ním nesusedia.

Dôkaz.

Uvažujme ľubovoľný trojuholník $EFG$. Nech má vonkajší uhol trojuholníka $FGQ$ (obr. 3).

Podľa vety 1 budeme mať $∠E+∠F+∠G=180^\circ$, teda,

$∠G=180^\circ-(∠E+∠F)$

Keďže uhol $FGQ$ je vonkajší, susedí s uhlom $∠G$

$∠FGQ=180^\circ-∠G=180^\circ-180^\circ+(∠E+∠F)=∠E+∠F$

Veta bola dokázaná.

Vzorové úlohy

Príklad 1

Nájdite všetky uhly trojuholníka, ak je rovnostranný.

Pretože všetky strany rovnostranného trojuholníka sú rovnaké, budeme mať za to, že všetky uhly v ňom sú tiež rovnaké. Označme ich miery pomocou $α$.

Potom podľa vety 1 dostaneme

$α+α+α=180^\circ$

Odpoveď: všetky uhly sa rovnajú $60^\circ$.

Príklad 2

Nájdite všetky uhly rovnoramenného trojuholníka, ak sa jeden z jeho uhlov rovná $100^\circ$.

Uveďme nasledujúce označenie uhlov v rovnoramennom trojuholníku:

Keďže v podmienke nie je presne dané, ktorému uhlu $100^\circ$ sa rovná, sú možné dva prípady:

Uhol rovný $100^\circ$ je uhol v základni trojuholníka.

Pomocou vety o uhloch na základni rovnoramenného trojuholníka získame

$∠2=∠3=100^\circ$

Ale potom bude len ich súčet väčší ako $180^\circ$, čo je v rozpore s podmienkami vety 1. To znamená, že tento prípad nenastane.

Uhol rovný $100^\circ$ je uhol medzi rovnakými stranami, tj

Po včerajšku:

Poďme sa hrať s mozaikou podľa rozprávky o geometrii:

Kedysi boli trojuholníky. Tak podobné, že sú len kópiami jeden druhého.
Nejako stáli vedľa seba v priamom rade. A keďže boli všetci rovnako vysokí -
potom boli ich vrcholy na rovnakej úrovni pod vládcom:

Trojuholníky milovali hádzať sa a stáť na hlavách. Vyliezli do horného radu a postavili sa na roh ako akrobati.
A my už vieme - keď stoja s vrcholmi presne v rade,
potom sa aj ich chodidlá riadia pravítkom - veď ak je niekto rovnako vysoký, tak je rovnako vysoký aj dolu hlavou!

Boli vo všetkom rovnakí – mali rovnakú výšku a rovnaké podrážky,
a šmykľavky po stranách – jedna strmšia, druhá plochejšia – majú rovnakú dĺžku
a majú rovnaký sklon. No proste dvojičky! (iba v inom oblečení, každý má svoj kúsok skladačky).

- Kde majú trojuholníky rovnaké strany? Kde sú rohy rovnaké?

Trojuholníky sa postavili na hlavu, stáli tam a rozhodli sa skĺznuť a ľahnúť si do spodného radu.
Šmýkali sa a šmýkali dolu kopcom; ale ich snímky sú rovnaké!
Zapadli teda presne medzi spodné trojuholníky, bez medzier a nikto nikoho neodstrčil.

Poobzerali sme sa po trojuholníkoch a všimli sme si zaujímavú vlastnosť.
Kdekoľvek sa ich uhly stretnú, všetky tri uhly sa určite stretnú:
najväčší je „hlavový uhol“, najostrejší uhol a tretí, stredne najväčší uhol.
Zviazali dokonca farebné stužky, aby bolo hneď zrejmé, ktorá je ktorá.

A ukázalo sa, že tri uhly trojuholníka, ak ich skombinujete -
vytvorte jeden veľký uhol, „otvorený roh“ – ako obálka otvorenej knihy,

_______________________O ____________________

nazýva sa to otočený uhol.

Akýkoľvek trojuholník je ako pas: tri uhly sa spolu rovnajú rozvinutému uhlu.
Niekto ti zaklope na dvere: - klop-klop, ja som trojuholník, nechaj ma prenocovať!
A ty mu povieš - Ukážte mi súčet uhlov v rozšírenej forme!
A hneď je jasné, či ide o skutočný trojuholník alebo podvodníka.
Overenie zlyhalo - Otočte o stoosemdesiat stupňov a choďte domov!

Keď hovoria „otočte sa o 180°“, znamená to otočiť sa dozadu a
ísť opačným smerom.

To isté v známejších výrazoch, bez „kedysi“:

Urobme rovnobežnú transláciu trojuholníka ABC pozdĺž osi OX
na vektor AB rovná dĺžke základne AB.
Priamka DF prechádzajúca vrcholmi C a C 1 trojuholníkov
rovnobežne s osou OX v dôsledku skutočnosti, že kolmá na os OX
úsečky h a h 1 (výšky rovnakých trojuholníkov) sú rovnaké.
Základňa trojuholníka A 2 B 2 C 2 je teda rovnobežná so základňou AB
a je rovná dĺžke (keďže vrchol C 1 je posunutý voči C o hodnotu AB).
Trojuholníky A 2 B 2 C 2 a ABC sú na troch stranách rovnaké.
Preto uhly ∠A 1 ∠B ∠C 2 zvierajúce priamy uhol sa rovnajú uhlom trojuholníka ABC.
=> Súčet uhlov trojuholníka je 180°

Pri pohyboch – „prekladoch“ je takzvaný dôkaz kratší a jasnejší,
kúskom mozaiky rozumie aj dieťa.

Ale tradičná škola:

založené na rovnosti vnútorných priečne ležiacich uhlov odrezaných na rovnobežných líniách

cenné v tom, že dáva predstavu o tom, prečo je to tak,
Prečo? súčet uhlov trojuholníka sa rovná opačnému uhlu?

Pretože inak by rovnobežné čiary nemali vlastnosti známe nášmu svetu.

Vety fungujú oboma smermi. Z axiómy rovnobežných priamok vyplýva
rovnosť priečne ležiacich a vertikálnych uhlov az nich - súčet uhlov trojuholníka.

Ale platí to aj naopak: pokiaľ sú uhly trojuholníka 180°, existujú rovnobežné čiary
(tak, že cez bod, ktorý neleží na priamke, možno nakresliť jedinečnú priamku || danej).
Ak sa jedného dňa na svete objaví trojuholník, ktorého súčet uhlov sa nerovná rozvinutému uhlu -
potom paralelné prestanú byť paralelné, celý svet bude ohnutý a pokrivený.

Ak sú pruhy s trojuholníkovými vzormi umiestnené nad sebou -
celé pole môžete pokryť opakujúcim sa vzorom, ako je podlaha s dlaždicami:

na takejto mriežke môžete obkresľovať rôzne tvary - šesťuholníky, kosoštvorce,
hviezdicové mnohouholníky a získajte rôzne parkety

Obkladanie lietadla parketami nie je len zábavná hra, ale aj relevantný matematický problém:

________________________________________ _______________________-------__________ ________________________________________ ______________
/\__||_/\__||_/\__||_/\__||_/\__|)0(|_/\__||_/\__||_/\__||_/\__||_/\=/\__||_/ \__||_/\__||_/\__||_/\__|)0(|_/\__||_/\__||_/\__||_/\__||_/\

Pretože každý štvoruholník je obdĺžnik, štvorec, kosoštvorec atď.,
môže byť zložený z dvoch trojuholníkov,
respektíve súčet uhlov štvoruholníka: 180° + 180° = 360°

Rovnaké rovnoramenné trojuholníky sa skladajú do štvorcov rôznymi spôsobmi.
Malý štvorec z 2 častí. Priemer 4. A najväčší z 8.
Koľko figúrok je na výkrese, ktorý pozostáva zo 6 trojuholníkov?

Ciele a ciele:

Vzdelávacie:

zopakovať a zovšeobecniť poznatky o trojuholníku;
dokážte vetu o súčte uhlov trojuholníka;
prakticky overiť správnosť formulácie vety;
naučiť sa aplikovať získané poznatky pri riešení problémov.

Vzdelávacie:

rozvíjať geometrické myslenie, záujem o predmet, kognitívnu a tvorivú činnosť žiakov, matematickú reč, schopnosť samostatne získavať poznatky.

Vzdelávacie:

rozvíjať osobné vlastnosti študentov, ako je odhodlanie, vytrvalosť, presnosť a schopnosť pracovať v tíme.

Vybavenie: multimediálny projektor, trojuholníky z farebného papiera, vzdelávací komplex „Živá matematika“, počítač, plátno.

Prípravná fáza: Učiteľ dá študentovi za úlohu pripraviť historickú poznámku o vete „Súčet uhlov trojuholníka“.

Typ lekcie: učenie sa nového materiálu.

Počas vyučovania

I. Organizačný moment

Pozdravujem. Psychologický postoj žiakov k práci.

II. Rozcvička

S geometrickým útvarom „trojuholník“ sme sa zoznámili v predchádzajúcich lekciách. Zopakujme si, čo vieme o trojuholníku?

Žiaci pracujú v skupinách. Dostávajú príležitosť navzájom komunikovať, každý samostatne budovať proces poznania.

Čo sa stalo? Každá skupina predloží svoje návrhy, učiteľ ich napíše na tabuľu. O výsledkoch sa diskutuje:

Obrázok 1

III. Formulovanie cieľa lekcie

Takže o trojuholníku už vieme dosť veľa. Ale nie všetky. Každý z vás má na stole trojuholníky a uhlomery. Aký druh problému si myslíte, že môžeme formulovať?

Žiaci formulujú úlohu hodiny - nájsť súčet uhlov trojuholníka.

IV. Vysvetlenie nového materiálu

Praktická časť(podporuje aktualizáciu vedomostí a sebapoznávacích zručností) Zmerajte uhly pomocou uhlomeru a nájdite ich súčet. Výsledky si zapíšte do zošita (vypočujte si prijaté odpovede). Zistíme, že súčet uhlov je u každého iný (môže sa to stať, pretože uhlomer nebol aplikovaný presne, výpočet bol vykonaný neopatrne atď.).

Zložte pozdĺž bodkovaných čiar a zistite, čomu sa ešte rovná súčet uhlov trojuholníka:

A)
Obrázok 2

b)
Obrázok 3

V)
Obrázok 4

G)
Obrázok 5

d)
Obrázok 6

Po ukončení praktickej práce žiaci formulujú odpoveď: Súčet uhlov trojuholníka sa rovná stupňovej miere rozvinutého uhla, teda 180°.

Učiteľ: V matematike praktická práca umožňuje len nejaké tvrdenie, ale treba to dokázať. Tvrdenie, ktorého platnosť je potvrdená dôkazom, sa nazýva teorém. Akú vetu môžeme sformulovať a dokázať?

študenti: Súčet uhlov trojuholníka je 180 stupňov.

Historický odkaz: Vlastnosť súčtu uhlov trojuholníka bola založená v starovekom Egypte. Dôkaz uvedený v moderných učebniciach je obsiahnutý v Proklovom komentári k Euklidovým prvkom. Proclus tvrdí, že tento dôkaz (obr. 8) objavili Pytagorejci (5. storočie pred Kristom). V prvej knihe Živly uvádza Euklides ďalší dôkaz vety o súčte uhlov trojuholníka, ktorý možno ľahko pochopiť pomocou nákresu (obr. 7):

Obrázok 7

Obrázok 8

Kresby sa zobrazujú na obrazovke cez projektor.

Učiteľ ponúka dôkaz vety pomocou nákresov.

Potom sa dôkaz uskutoční pomocou učebného a vzdelávacieho komplexu „Živá matematika“. Učiteľ premietne dôkaz vety na počítači.

Veta o súčte uhlov trojuholníka: „Súčet uhlov trojuholníka je 180°“

Obrázok 9

dôkaz:

A)

Obrázok 10

b)

Obrázok 11

V)

Obrázok 12

Študenti si do zošitov stručne poznačia dôkaz vety:

Veta: Súčet uhlov trojuholníka je 180°.

Obrázok 13

Vzhľadom na to:Δ ABC

dokázať: A + B + C = 180°.

dôkaz:

Čo bolo potrebné dokázať.

V. Phys. len minútu.

VI. Vysvetlenie nového materiálu (pokračovanie)

Dôsledok z vety o súčte uhlov trojuholníka si študenti odvodzujú samostatne, čo prispieva k rozvoju schopnosti formulovať svoj vlastný názor, vyjadrovať sa a argumentovať zaň:

V akomkoľvek trojuholníku sú buď všetky uhly ostré, alebo dva sú ostré a tretí je tupý alebo pravý..

Ak má trojuholník všetky ostré uhly, potom sa nazýva ostrý uhol.

Ak je jeden z uhlov trojuholníka tupý, potom sa nazýva tupo-uhlové.

Ak je jeden z uhlov trojuholníka pravý, potom sa nazýva pravouhlý.

Veta o súčte uhlov trojuholníka nám umožňuje triediť trojuholníky nielen podľa strán, ale aj podľa uhlov. (Keď študenti predstavia typy trojuholníkov, študenti vyplnia tabuľku)

stôl 1

Trojuholníkový pohľad	Rovnoramenné	Rovnostranný	Všestranný
Obdĺžnikový
Tupý
Ostrý uhlový

VII. Konsolidácia študovaného materiálu.

Riešte problémy ústne:

(Výkresy sa zobrazujú na obrazovke cez projektor)

Úloha 1. Nájdite uhol C.

Obrázok 14

Úloha 2. Nájdite uhol F.

Obrázok 15

Úloha 3. Nájdite uhly K a N.

Obrázok 16

Úloha 4. Nájdite uhly P a T.

Obrázok 17

Úlohu č. 223 (b, d) vyriešte sami.
Vyriešte úlohu na tabuli a do zošitov, žiak č.224.
Otázky: Môže mať trojuholník: a) dva pravé uhly; b) dva tupé uhly; c) jeden pravý a jeden tupý uhol.
(vykonané ústne) Karty na každom stole zobrazujú rôzne trojuholníky. Určite okom typ každého trojuholníka.

Obrázok 18