Satz über die Winkelsumme eines Dreiecks. Winkelsumme eines Dreiecks. Satz über die Winkelsumme eines Dreiecks Warum beträgt die Winkelsumme eines Dreiecks 180?

Satz. Die Summe der Innenwinkel eines Dreiecks entspricht zwei rechten Winkeln.

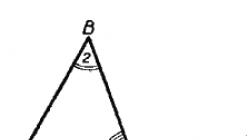
Nehmen wir ein Dreieck ABC (Abb. 208). Bezeichnen wir seine Innenwinkel mit den Zahlen 1, 2 und 3. Beweisen wir das

∠1 + ∠2 + ∠3 = 180°.

Zeichnen wir durch einen Eckpunkt des Dreiecks, zum Beispiel B, eine gerade Linie MN parallel zu AC.

Am Scheitelpunkt B haben wir drei Winkel: ∠4, ∠2 und ∠5. Ihre Summe ist ein gerader Winkel, also gleich 180°:

∠4 + ∠2 + ∠5 = 180°.

Aber ∠4 = ∠1 sind interne Kreuzwinkel mit Parallelen MN und AC und Sekante AB.

∠5 = ∠3 – das sind innere Kreuzwinkel mit Parallelen MN und AC und Sekante BC.

Das bedeutet, dass ∠4 und ∠5 durch ihre Gleichen ∠1 und ∠3 ersetzt werden können.

Daher ist ∠1 + ∠2 + ∠3 = 180°. Der Satz ist bewiesen.

2. Eigenschaft des Außenwinkels eines Dreiecks.

Satz. Ein Außenwinkel eines Dreiecks ist gleich der Summe zweier Innenwinkel, die nicht an das Dreieck angrenzen.

Tatsächlich ist im Dreieck ABC (Abb. 209) ∠1 + ∠2 = 180° - ∠3, aber auch ∠ВСD, der Außenwinkel dieses Dreiecks, der nicht an ∠1 und ∠2 angrenzt, ebenfalls gleich 180° - ∠3 .

Auf diese Weise:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Daher ist ∠1 + ∠2= ∠BCD.

Die abgeleitete Eigenschaft des Außenwinkels eines Dreiecks verdeutlicht den Inhalt des zuvor bewiesenen Satzes über den Außenwinkel eines Dreiecks, der lediglich besagte, dass der Außenwinkel eines Dreiecks größer ist als jeder Innenwinkel eines nicht angrenzenden Dreiecks; Nun steht fest, dass der Außenwinkel gleich der Summe der beiden nicht an ihn angrenzenden Innenwinkel ist.

3. Eigenschaft eines rechtwinkligen Dreiecks mit einem Winkel von 30°.

Satz. Ein Schenkel eines rechtwinkligen Dreiecks, der einem Winkel von 30° gegenüberliegt, ist gleich der halben Hypotenuse.

Der Winkel B im rechtwinkligen Dreieck ACB sei gleich 30° (Abb. 210). Dann beträgt sein anderer spitzer Winkel 60°.

Beweisen wir, dass das Bein AC gleich der Hälfte der Hypotenuse AB ist. Lassen Sie uns den Schenkel AC über den Scheitelpunkt des rechten Winkels C hinaus verlängern und ein Segment CM gleich dem Segment AC beiseite legen. Verbinden wir Punkt M mit Punkt B. Das resultierende Dreieck ВСМ ist gleich dem Dreieck ACB. Wir sehen, dass jeder Winkel des Dreiecks ABM gleich 60° ist, daher ist dieses Dreieck ein gleichseitiges Dreieck.

Das Bein AC ist gleich der halben Hypotenuse AB, und da AM gleich AB ist, ist das Bein AC gleich der halben Hypotenuse AB.

Können Sie beweisen, dass die Winkelsumme in einem Dreieck 180 Grad beträgt? und bekam die beste Antwort

Antwort von Top_ed[Guru]
Warum etwas beweisen, was schon vor sehr, sehr langer Zeit bewiesen wurde?
Der Dreieckswinkelsummensatz, ein klassischer Satz der euklidischen Geometrie, besagt dies
Die Winkelsumme eines Dreiecks beträgt 180°.
Sei ABC ein beliebiges Dreieck. Zeichnen wir eine Linie durch den Scheitelpunkt B parallel zur Linie AC. Markieren wir Punkt D darauf, sodass die Punkte A und D auf gegenüberliegenden Seiten der Linie BC liegen.
Die Winkel DBC und ACB sind kongruent als innere, kreuzende Winkel, die durch die Querlinie BC mit den parallelen Linien AC und BD gebildet werden. Daher ist die Summe der Winkel eines Dreiecks an den Eckpunkten B und C gleich dem Winkel ABD.
Die Summe aller drei Winkel eines Dreiecks ist gleich der Summe der Winkel ABD und BAC. Da es sich um einseitige Innenwinkel für Parallel AC und BD und Sekante AB handelt, beträgt deren Summe 180°. Der Satz ist bewiesen.

Antwort von Boriska(c)[Guru]
Ich kann, aber ich weiß nicht mehr wie))

Antwort von Murashkina[Guru]
Dürfen. Ist es für Sie dringend? ? Machst du die Prüfung für die fünfte Klasse? ? :))

Antwort von Oriy Semykin[Guru]
1. Es hängt von der Geometrie des Raums ab. Auf der Riemannschen Ebene > 180, auf dem Quadrat. Lobatschewski< 180. На Эвклидовой - равенство.
2. Zeichnen Sie eine Linie durch den Scheitelpunkt parallel zu einer der Seiten und untersuchen Sie die Kreuzwinkel, die von den beiden Seiten und der zusätzlichen Linie gebildet werden. Der resultierende Winkel (180) ist gleich der Summe der drei Winkel des Dreiecks.

Der Beweis beruht im Wesentlichen auf der Tatsache, dass nur eine parallele Linie gezeichnet werden kann. Es gibt viele Geometrien, bei denen dies nicht der Fall ist.

Antwort von Yuri[Guru]
Warum beweisen, was bewiesen wurde?)) Schneiden Sie das Quadrat in zwei Teile, wenn Sie etwas Neues wollen))

Antwort von Nikolay Evgenievich[Guru]
Ich kann nicht.

Antwort von Alex Brichka[Experte]
Ja, hier gibt es nichts zu beweisen, Sie müssen nur Winkel zueinander addieren und das war’s.

Antwort von 2 Antworten[Guru]

Hallo! Hier finden Sie eine Auswahl an Themen mit Antworten auf Ihre Frage: Können Sie beweisen, dass die Winkelsumme in einem Dreieck 180 Grad beträgt?

Vorabinformationen

Schauen wir uns zunächst das Konzept eines Dreiecks direkt an.

Definition 1

Wir nennen ein Dreieck eine geometrische Figur, die aus drei Punkten besteht, die durch Segmente miteinander verbunden sind (Abb. 1).

Definition 2

Im Rahmen der Definition 1 nennen wir die Punkte die Eckpunkte des Dreiecks.

Definition 3

Im Rahmen der Definition 1 werden die Segmente Seiten des Dreiecks genannt.

Offensichtlich hat jedes Dreieck drei Eckpunkte und drei Seiten.

Satz über die Winkelsumme in einem Dreieck

Lassen Sie uns einen der wichtigsten Sätze im Zusammenhang mit Dreiecken einführen und beweisen, nämlich den Satz über die Winkelsumme in einem Dreieck.

Satz 1

Die Winkelsumme in jedem beliebigen Dreieck beträgt $180^\circ$.

Nachweisen.

Betrachten Sie das Dreieck $EGF$. Beweisen wir, dass die Winkelsumme in diesem Dreieck $180^\circ$ beträgt. Machen wir eine zusätzliche Konstruktion: Zeichnen Sie die gerade Linie $XY||EG$ (Abb. 2)

Da die Geraden $XY$ und $EG$ parallel sind, liegen $∠E=∠XFE$ kreuzweise an der Sekante $FE$ und $∠G=∠YFG$ kreuzweise an der Sekante $FG$

Der Winkel $XFY$ wird umgekehrt und beträgt daher $180^\circ$.

$∠XFY=∠XFE+∠F+∠YFG=180^\circ$

Somit

$∠E+∠F+∠G=180^\circ$

Der Satz ist bewiesen.

Satz über den Außenwinkel eines Dreiecks

Ein weiterer Satz über die Winkelsumme eines Dreiecks kann als Satz über den Außenwinkel betrachtet werden. Lassen Sie uns zunächst dieses Konzept vorstellen.

Definition 4

Wir nennen einen Außenwinkel eines Dreiecks einen Winkel, der an jeden Winkel des Dreiecks angrenzt (Abb. 3).

Betrachten wir nun den Satz direkt.

Satz 2

Ein Außenwinkel eines Dreiecks ist gleich der Summe zweier Winkel des Dreiecks, die nicht an ihn angrenzend sind.

Nachweisen.

Betrachten Sie ein beliebiges Dreieck $EFG$. Es soll einen Außenwinkel des Dreiecks $FGQ$ haben (Abb. 3).

Nach Satz 1 erhalten wir $∠E+∠F+∠G=180^\circ$, also

$∠G=180^\circ-(∠E+∠F)$

Da der Winkel $FGQ$ extern ist, grenzt er dann an den Winkel $∠G$

$∠FGQ=180^\circ-∠G=180^\circ-180^\circ+(∠E+∠F)=∠E+∠F$

Der Satz ist bewiesen.

Beispielaufgaben

Beispiel 1

Finden Sie alle Winkel eines Dreiecks, wenn es gleichseitig ist.

Da alle Seiten eines gleichseitigen Dreiecks gleich sind, sind auch alle Winkel darin gleich. Bezeichnen wir ihre Gradmaße mit $α$.

Dann erhalten wir nach Satz 1

$α+α+α=180^\circ$

Antwort: Alle Winkel sind gleich $60^\circ$.

Beispiel 2

Finden Sie alle Winkel eines gleichschenkligen Dreiecks, wenn einer seiner Winkel gleich $100^\circ$ ist.

Führen wir die folgende Notation für Winkel in einem gleichschenkligen Dreieck ein:

Da wir in der Bedingung nicht genau angeben, welcher Winkel $100^\circ$ gleich ist, sind zwei Fälle möglich:

Ein Winkel gleich $100^\circ$ ist der Winkel an der Basis des Dreiecks.

Mit dem Satz über Winkel an der Basis eines gleichschenkligen Dreiecks erhalten wir:

$∠2=∠3=100^\circ$

Dann wird aber nur ihre Summe größer als $180^\circ$ sein, was den Bedingungen von Satz 1 widerspricht. Dies bedeutet, dass dieser Fall nicht auftritt.

Ein Winkel gleich $100^\circ$ ist der Winkel zwischen gleichen Seiten

Im Anschluss an gestern:

Spielen wir mit einem Mosaik, das auf einem Geometriemärchen basiert:

Es waren einmal Dreiecke. So ähnlich, dass sie nur Kopien voneinander sind.
Sie standen irgendwie in einer geraden Linie nebeneinander. Und da sie alle gleich groß waren -
dann waren ihre Spitzen auf gleicher Höhe, unter dem Lineal:

Dreiecke liebten es, zu stolpern und auf dem Kopf zu stehen. Sie kletterten in die oberste Reihe und stellten sich wie Akrobaten an die Ecke.
Und wir wissen es bereits – wenn sie mit ihren Spitzen genau in einer Linie stehen,
dann folgen auch ihre Fußsohlen einem Lineal – denn wenn jemand gleich groß ist, dann sind sie auch auf dem Kopf gleich groß!

Sie waren in allem gleich – die gleiche Höhe und die gleichen Sohlen,
und die Rutschen an den Seiten – eine steiler, die andere flacher – sind gleich lang
und sie haben die gleiche Steigung. Nun ja, nur Zwillinge! (nur in unterschiedlicher Kleidung, jedes mit seinem eigenen Puzzleteil).

- Wo haben die Dreiecke identische Seiten? Wo sind die Ecken gleich?

Die Dreiecke stellten sich auf den Kopf, standen da und beschlossen, abzurutschen und sich in die unterste Reihe zu legen.
Sie rutschten und rutschten einen Hügel hinunter; aber ihre Folien sind die gleichen!
So passen sie genau und lückenlos zwischen die unteren Dreiecke und niemand hat jemanden beiseite geschoben.

Wir schauten uns in den Dreiecken um und bemerkten eine interessante Besonderheit.
Wo auch immer ihre Blickwinkel zusammenkommen, werden sich mit Sicherheit alle drei Blickwinkel treffen:
der größte ist der „Kopfwinkel“, der spitzeste Winkel und der drittgrößte der mittlere.
Sie banden sogar farbige Bänder fest, damit man sofort erkennen konnte, wer welcher war.

Und es stellte sich heraus, dass die drei Winkel des Dreiecks, wenn man sie kombiniert -
einen großen Winkel bilden, eine „offene Ecke“ – wie der Einband eines offenen Buches,

______________________Ö ___________________

man nennt es einen gedrehten Winkel.

Jedes Dreieck ist wie ein Reisepass: Drei Winkel zusammen ergeben den aufgeklappten Winkel.
Jemand klopft an deine Tür: - Klopf-klopf, ich bin ein Dreieck, lass mich die Nacht verbringen!
Und du sagst ihm - Zeigen Sie mir die Summe der Winkel in erweiterter Form!
Und es ist sofort klar, ob es sich um ein echtes Dreieck oder um einen Hochstapler handelt.
Verifizierung fehlgeschlagen – Drehen Sie sich um 180 Grad und gehen Sie nach Hause!

Wenn man „um 180° drehen“ sagt, bedeutet das, dass man sich rückwärts dreht und
in die entgegengesetzte Richtung gehen.

Das Gleiche in bekannteren Ausdrücken, ohne „Es war einmal“:

Führen wir eine Parallelverschiebung des Dreiecks ABC entlang der OX-Achse durch
zum Vektor AB gleich der Länge der Basis AB.
Linie DF, die durch die Eckpunkte C und C 1 von Dreiecken verläuft
parallel zur OX-Achse, da senkrecht zur OX-Achse
Die Segmente h und h 1 (Höhen gleicher Dreiecke) sind gleich.
Somit ist die Basis des Dreiecks A 2 B 2 C 2 parallel zur Basis AB
und gleich lang (da der Scheitelpunkt C 1 relativ zu C um den Betrag AB verschoben ist).
Die Dreiecke A 2 B 2 C 2 und ABC sind auf drei Seiten gleich.
Daher sind die Winkel ∠A 1 ∠B ∠C 2, die einen geraden Winkel bilden, gleich den Winkeln des Dreiecks ABC.
=> Die Winkelsumme eines Dreiecks beträgt 180°

Bei Bewegungen – „Übersetzungen“ – ist der sogenannte Beweis kürzer und klarer,
Selbst ein Kind kann die Mosaiksteine verstehen.

Aber traditionelle Schule:

basierend auf der Gleichheit der inneren, kreuzliegenden Winkel, die auf parallelen Linien abgeschnitten werden

wertvoll, weil es eine Vorstellung davon gibt, warum das so ist,
Warum Die Summe der Winkel eines Dreiecks ist gleich dem Umkehrwinkel?

Denn sonst hätten parallele Linien nicht die Eigenschaften, die wir in unserer Welt kennen.

Die Theoreme funktionieren in beide Richtungen. Aus dem Axiom der parallelen Geraden folgt es
Gleichheit der quer liegenden und vertikalen Winkel und daraus - die Summe der Winkel eines Dreiecks.

Aber auch das Gegenteil ist der Fall: Solange die Winkel eines Dreiecks 180° betragen, gibt es parallele Linien
(so dass man durch einen Punkt, der nicht auf einer Geraden liegt, eine eindeutige Gerade || des gegebenen Punktes zeichnen kann).
Wenn eines Tages ein Dreieck auf der Welt erscheint, dessen Winkelsumme nicht dem aufgeklappten Winkel entspricht –
dann werden die Parallelen aufhören, parallel zu sein, die ganze Welt wird gebogen und schief sein.

Wenn Streifen mit Dreiecksmuster übereinander gelegt werden -
Sie können das gesamte Feld mit einem sich wiederholenden Muster bedecken, wie einen Boden mit Fliesen:

Sie können auf einem solchen Gitter verschiedene Formen nachzeichnen - Sechsecke, Rauten,
Sternpolygone und erhalten Sie eine Vielzahl von Parketten

Ein Flugzeug mit Parkett zu belegen ist nicht nur ein unterhaltsames Spiel, sondern auch ein relevantes mathematisches Problem:

________________________________________ _______________________-------__________ ________________________________________ ______________
/\__||_/\__||_/\__||_/\__||_/\__|)0(|_/\__||_/\__||_/\__||_/\__||_/\=/\__||_/ \__||_/\__||_/\__||_/\__|)0(|_/\__||_/\__||_/\__||_/\__||_/\

Da jedes Viereck ein Rechteck, ein Quadrat, eine Raute usw. ist,
kann aus zwei Dreiecken bestehen,
bzw. die Summe der Winkel eines Vierecks: 180° + 180° = 360°

Identische gleichschenklige Dreiecke werden auf unterschiedliche Weise zu Quadraten gefaltet.
Ein kleines Quadrat aus 2 Teilen. Durchschnittlich 4. Und der größte der 8.
Wie viele Figuren enthält die Zeichnung, bestehend aus 6 Dreiecken?

Ziele und Ziele:

Lehrreich:

Wissen über das Dreieck wiederholen und verallgemeinern;
Beweisen Sie den Satz über die Winkelsumme eines Dreiecks;
die Richtigkeit der Formulierung des Theorems praktisch überprüfen;
lernen, erworbenes Wissen bei der Lösung von Problemen anzuwenden.

Lehrreich:

Entwickeln Sie geometrisches Denken, Interesse am Thema, kognitive und kreative Aktivität der Schüler, mathematische Sprache und die Fähigkeit, sich selbstständig Wissen anzueignen.

Lehrreich:

Entwickeln Sie die persönlichen Qualitäten der Schüler wie Entschlossenheit, Ausdauer, Genauigkeit und die Fähigkeit, im Team zu arbeiten.

Ausrüstung: Multimedia-Projektor, Dreiecke aus farbigem Papier, Bildungskomplex „Living Mathematics“, Computer, Leinwand.

Vorbereitungsphase: Der Lehrer gibt dem Schüler die Aufgabe, eine historische Notiz zum Satz „Winkelsumme eines Dreiecks“ anzufertigen.

Unterrichtsart: Neues Material lernen.

Während des Unterrichts

I. Organisatorischer Moment

Grüße. Psychologische Einstellung der Studierenden zur Arbeit.

II. Sich warm laufen

Die geometrische Figur „Dreieck“ haben wir in früheren Lektionen kennengelernt. Wiederholen wir, was wir über das Dreieck wissen?

Die Studierenden arbeiten in Gruppen. Sie erhalten die Möglichkeit, miteinander zu kommunizieren, um den Erkenntnisprozess unabhängig voneinander aufzubauen.

Was ist passiert? Jede Gruppe macht ihre Vorschläge, der Lehrer schreibt sie an die Tafel. Die Ergebnisse werden besprochen:

Bild 1

III. Das Unterrichtsziel formulieren

Wir wissen also schon ziemlich viel über das Dreieck. Aber nicht alles. Jeder von euch hat Dreiecke und Winkelmesser auf seinem Schreibtisch. Was für ein Problem können wir Ihrer Meinung nach formulieren?

Die Schüler formulieren die Aufgabe der Lektion – die Summe der Winkel eines Dreiecks zu ermitteln.

IV. Erläuterung des neuen Materials

Praktischer Teil(Fördert die Aktualisierung von Wissen und Selbsterkenntnisfähigkeiten.) Messen Sie die Winkel mit einem Winkelmesser und ermitteln Sie ihre Summe. Notieren Sie die Ergebnisse in Ihrem Notizbuch (hören Sie sich die erhaltenen Antworten an). Wir stellen fest, dass die Summe der Winkel bei jedem unterschiedlich ist (dies kann passieren, weil der Winkelmesser nicht genau angesetzt wurde, die Berechnung nachlässig durchgeführt wurde usw.).

Falten Sie entlang der gestrichelten Linien und finden Sie heraus, wie groß die Winkelsumme eines Dreiecks sonst noch ist:

A)
Figur 2

B)
Figur 3

V)
Figur 4

G)
Abbildung 5

D)
Abbildung 6

Nach Abschluss der praktischen Arbeit formulieren die Studierenden die Antwort: Die Winkelsumme eines Dreiecks ist gleich dem Gradmaß des aufgefalteten Winkels, also 180°.

Lehrer: In der Mathematik lässt sich durch praktische Arbeit nur eine Aussage treffen, die aber bewiesen werden muss. Eine Aussage, deren Gültigkeit durch Beweise nachgewiesen wird, wird als Theorem bezeichnet. Welchen Satz können wir formulieren und beweisen?

Studenten: Die Winkelsumme eines Dreiecks beträgt 180 Grad.

Historischer Bezug: Die Eigenschaft der Winkelsumme eines Dreiecks wurde im alten Ägypten festgestellt. Der in modernen Lehrbüchern dargelegte Beweis ist im Kommentar von Proklos zu Euklids Elementen enthalten. Proklos behauptet, dass dieser Beweis (Abb. 8) von den Pythagoräern (5. Jahrhundert v. Chr.) entdeckt wurde. Im ersten Buch der Elemente führt Euklid einen weiteren Beweis des Satzes über die Winkelsumme eines Dreiecks an, der anhand einer Zeichnung leicht verständlich ist (Abb. 7):

Abbildung 7

Abbildung 8

Die Zeichnungen werden über einen Projektor auf der Leinwand angezeigt.

Der Lehrer bietet an, den Satz anhand von Zeichnungen zu beweisen.

Anschließend erfolgt der Beweis mithilfe des Lehr- und Lernkomplexes „Living Mathematics“.. Der Lehrer projiziert den Beweis des Theorems auf den Computer.

Satz über die Winkelsumme eines Dreiecks: „Die Winkelsumme eines Dreiecks beträgt 180°“

Abbildung 9

Nachweisen:

A)

Abbildung 10

B)

Abbildung 11

V)

Abbildung 12

Die Schüler notieren kurz den Beweis des Satzes in ihren Notizbüchern:

Satz: Die Winkelsumme eines Dreiecks beträgt 180°.

Abbildung 13

Gegeben:ΔABC

Beweisen: A + B + C = 180°.

Nachweisen:

Was bewiesen werden musste.

V. Phys. nur eine Minute.

VI. Erläuterung des neuen Materials (Fortsetzung)

Die Folgerung aus dem Satz über die Winkelsumme eines Dreiecks wird von den Studierenden selbstständig abgeleitet, dies trägt zur Entwicklung der Fähigkeit bei, den eigenen Standpunkt zu formulieren, ihn auszudrücken und zu argumentieren:

In jedem Dreieck sind entweder alle Winkel spitz oder zwei sind spitz und der dritte ist stumpf oder rechtwinklig..

Wenn ein Dreieck alle spitzen Winkel hat, heißt es spitzwinklig.

Wenn einer der Winkel eines Dreiecks stumpf ist, heißt es stumpfwinklig.

Wenn einer der Winkel eines Dreiecks recht ist, heißt es rechteckig.

Der Satz über die Winkelsumme eines Dreiecks ermöglicht es uns, Dreiecke nicht nur nach Seiten, sondern auch nach Winkeln zu klassifizieren. (Während die Schüler Dreieckstypen vorstellen, füllen sie die Tabelle aus)

Tabelle 1

Dreiecksansicht	Gleichschenklige	Gleichseitig	Vielseitig
Rechteckig
Stumpf
Spitzwinklig

VII. Konsolidierung des untersuchten Materials.

Probleme mündlich lösen:

(Zeichnungen werden über einen Projektor auf der Leinwand angezeigt)

Aufgabe 1. Finden Sie den Winkel C.

Abbildung 14

Aufgabe 2. Finden Sie den Winkel F.

Abbildung 15

Aufgabe 3. Finden Sie die Winkel K und N.

Abbildung 16

Aufgabe 4. Finden Sie die Winkel P und T.

Abbildung 17

Lösen Sie Aufgabe Nr. 223 (b, d) selbst.
Lösen Sie das Problem an der Tafel und in Notizbüchern, Schüler Nr. 224.
Fragen: Kann ein Dreieck haben: a) zwei rechte Winkel; b) zwei stumpfe Winkel; c) ein rechter und ein stumpfer Winkel.
(mündlich durchgeführt) Die Karten auf jedem Tisch zeigen verschiedene Dreiecke. Bestimmen Sie mit dem Auge den Typ jedes Dreiecks.

Abbildung 18