Tétel a háromszög szögeinek összegéről. Egy háromszög szögeinek összege. Tétel a háromszög szögeinek összegéről Miért 180 a háromszög szögösszege?

Tétel. Egy háromszög belső szögeinek összege két derékszöggel egyenlő.

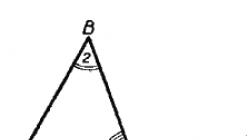
Vegyünk egy ABC háromszöget (208. ábra). Jelöljük belső szögeit 1, 2 és 3 számokkal. Bizonyítsuk be

∠1 + ∠2 + ∠3 = 180°.

Rajzoljunk át a háromszög valamelyik csúcsán, például B-n, egy AC-vel párhuzamos MN egyenest.

A B csúcsban három szöget kaptunk: ∠4, ∠2 és ∠5. Összegük egyenes szög, ezért egyenlő 180°-kal:

∠4 + ∠2 + ∠5 = 180°.

De ∠4 = ∠1 belső keresztirányú szögek MN és AC párhuzamos egyenesekkel és AB szekánssal.

∠5 = ∠3 - ezek belső keresztirányú szögek MN és AC párhuzamos egyenesekkel és BC szekánssal.

Ez azt jelenti, hogy ∠4 és ∠5 helyettesíthető ∠1 és ∠3 értékekkel.

Ezért ∠1 + ∠2 + ∠3 = 180°. A tétel bizonyítást nyert.

2. Háromszög külső szögének tulajdonsága.

Tétel. Egy háromszög külső szöge egyenlő két olyan belső szög összegével, amelyek nem szomszédosak vele.

Valójában az ABC háromszögben (209. ábra) ∠1 + ∠2 = 180° - ∠3, de ∠ВСD is ennek a háromszögnek a külső szöge, amely nem szomszédos ∠1 és ∠2, szintén 180°. -∠3.

És így:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Ezért ∠1 + ∠2= ∠BCD.

A háromszög külső szögének származtatott tulajdonsága tisztázza a háromszög külső szögére vonatkozó, korábban bizonyított tétel tartalmát, amely csak azt mondta ki, hogy a háromszög külső szöge nagyobb, mint a vele nem szomszédos háromszög minden belső szöge; most megállapítottuk, hogy a külső szög egyenlő a vele nem szomszédos két belső szög összegével.

3. 30°-os szögű derékszögű háromszög tulajdonsága.

Tétel. Egy derékszögű háromszög 30°-os szöggel szemben fekvő szára egyenlő a befogó felével.

Legyen B szög az ACB derékszögű háromszögben 30° (210. ábra). Ekkor a másik hegyesszöge 60° lesz.

Bizonyítsuk be, hogy az AC láb egyenlő az AB hipotenusz felével. Hosszabbítsuk meg az AC szakaszt a C derékszög csúcsán túl, és tegyünk félre egy CM szakaszt, amely megegyezik az AC szakasszal. Kössük össze az M pontot a B ponttal. A kapott ВСМ háromszög egyenlő az ACB háromszöggel. Látjuk, hogy az ABM háromszög minden szöge 60°, ezért ez a háromszög egyenlő oldalú háromszög.

Az AC láb egyenlő az AM felével, és mivel AM egyenlő az AB-vel, az AC láb egyenlő az AB hipotenusz felével.

Be tudod bizonyítani, hogy egy háromszög szögeinek összege 180 fokkal? és megkapta a legjobb választ

Top_ed[guru] válasza
Minek bizonyítani valamit, ami már nagyon-nagyon régen bebizonyosodott.
A háromszög szögösszeg tétele, az euklideszi geometria klasszikus tétele kimondja, hogy
Egy háromszög szögeinek összege 180°.
Legyen ABC tetszőleges háromszög. Rajzoljunk egy egyenest a B csúcson keresztül párhuzamosan az AC egyenessel. Jelöljük rajta a D pontot úgy, hogy az A és D pont a BC egyenes ellentétes oldalán legyen.
A DBC és ACB szögek egybevágóak, mint belső keresztben fekvő szögek, amelyeket a keresztirányú BC alkot az AC és BD párhuzamos egyenesekkel. Ezért a háromszög szögeinek összege a B és C csúcsokban egyenlő az ABD szöggel.
A háromszög mindhárom szögének összege egyenlő az ABD és BAC szögek összegével. Mivel ezek egyoldalú belső szögek párhuzamos AC és BD és AB szekáns esetén, ezek összege 180°. A tétel bizonyítást nyert.

Válasz tőle Boriska(c)[guru]
Megtehetem, de nem emlékszem hogyan))

Válasz tőle Muraskina[guru]
Tud. Sürgős neked? ? Ötödik osztályos vizsgát teszel? ? :))

Válasz tőle Oriy Semykin[guru]
1. A tér geometriájától függ. A Riemann síkon > 180, a téren. Lobacsevszkij< 180. На Эвклидовой - равенство.
2. A csúcson keresztül húzz egy egyenest az egyik oldallal párhuzamosan, és vizsgáld meg a két oldal és a járulékos egyenes által alkotott keresztirányú szögeket! A kapott szög (180) egyenlő a háromszög három szögének összegével.

A bizonyítás lényegében azon alapul, hogy csak egy párhuzamos egyenes húzható. Nagyon sok geometria van, ahol ez nem így van.

Válasz tőle Yuri[guru]
Minek bizonygatni azt, ami bevált?)) Vágja két részre a négyzetet, ha valami újat szeretne))

Válasz tőle Nyikolaj Jevgenyevics[guru]
Nem tudok.

Válasz tőle Alex Brichka[szakértő]
Igen, itt nincs mit bizonyítani, csak szögeket kell adni egymáshoz, és ennyi.

Válasz tőle 2 válasz[guru]

Helló! Íme néhány téma a válaszokkal a kérdésedre: Be tudod bizonyítani, hogy egy háromszög szögeinek összege 180 fokkal egyenlő?

Előzetes információ

Először nézzük közvetlenül a háromszög fogalmát.

1. definíció

Háromszögnek nevezzük azt a geometriai alakzatot, amely három, egymással szakaszokkal összekapcsolt pontból áll (1. ábra).

2. definíció

Az 1. definíció keretein belül a pontokat a háromszög csúcsainak nevezzük.

3. definíció

Az 1. definíció keretein belül a szakaszokat a háromszög oldalainak nevezzük.

Nyilvánvaló, hogy minden háromszögnek 3 csúcsa és három oldala van.

Tétel a háromszög szögeinek összegéről

Vezessük be és bizonyítsuk be a háromszögekkel kapcsolatos egyik fő tételt, mégpedig a háromszög szögeinek összegére vonatkozó tételt.

1. tétel

A szögek összege bármely tetszőleges háromszögben $180^\circ$.

Bizonyíték.

Tekintsük az $EGF$ háromszöget. Bizonyítsuk be, hogy ebben a háromszögben a szögek összege $180^\circ$. Készítsünk egy további konstrukciót: húzzuk meg a $XY||EG$ egyenest (2. ábra)

Mivel a $XY$ és $EG$ egyenesek párhuzamosak, ezért a $∠E=∠XFE$ a $FE$ szekánsnál keresztben, a $∠G=∠YFG$ pedig a $FG$ szekánsnál keresztben fekszik.

A(z) $XFY$ szög megfordul, ezért 180$^\circ$ lesz.

$∠XFY=∠XFE+∠F+∠YFG=180^\circ$

Ennélfogva

$∠E+∠F+∠G=180^\circ$

A tétel bizonyítást nyert.

Háromszög külső szög tétel

Egy másik, a háromszög szögösszegére vonatkozó tétel tekinthető a külső szögre vonatkozó tételnek. Először is mutassuk be ezt a fogalmat.

4. definíció

A háromszög külső szögének azt a szöget fogjuk nevezni, amely a háromszög bármely szögével szomszédos (3. ábra).

Tekintsük most közvetlenül a tételt.

2. tétel

Egy háromszög külső szöge egyenlő a háromszög két olyan szögének összegével, amelyek nem szomszédosak vele.

Bizonyíték.

Tekintsünk egy tetszőleges $EFG$ háromszöget. Legyen a $FGQ$ háromszög külső szöge (3. ábra).

Az 1. Tétel szerint $∠E+∠F+∠G=180^\circ$, tehát

$∠G=180^\circ-(∠E+∠F)$

Mivel a $FGQ$ szög külső, ezért szomszédos a $∠G$ szöggel

$∠FGQ=180^\circ-∠G=180^\circ-180^\circ+(∠E+∠F)=∠E+∠F$

A tétel bizonyítást nyert.

Minta feladatok

1. példa

Határozza meg a háromszög összes szögét, ha egyenlő oldalú.

Mivel egy egyenlő oldalú háromszög minden oldala egyenlő, akkor azt fogjuk kapni, hogy minden szöge egyenlő egymással. Jelöljük a mértéküket $α$-val.

Ekkor az 1. tételből kapjuk

$α+α+α=180^\circ$

Válasz: minden szög egyenlő $60^\circ$.

2. példa

Keresse meg egy egyenlő szárú háromszög összes szögét, ha az egyik szöge egyenlő $100^\circ$.

Vezessük be a következő jelölést az egyenlő szárú háromszög szögeire:

Mivel abban a feltételben nincs megadva, hogy pontosan mekkora $100^\circ$ szöggel egyenlő, két eset lehetséges:

A $100^\circ$-nak megfelelő szög a háromszög alapjában lévő szög.

Az egyenlő szárú háromszög alapjában lévő szögekre vonatkozó tételt felhasználva megkapjuk

$∠2=∠3=100^\circ$

De akkor csak az összegük lesz nagyobb 180$^\circ$-nál, ami ellentmond az 1. Tétel feltételeinek. Ez azt jelenti, hogy ez az eset nem fordul elő.

A $100^\circ$-nak megfelelő szög az egyenlő oldalak közötti szög, azaz

A tegnapi folytatás:

Játsszunk egy geometria mese alapján készült mozaikkal:

Voltak egyszer háromszögek. Annyira hasonlítanak egymásra, hogy csak másolatai egymásnak.
Valahogy egyenes vonalban álltak egymás mellett. És mivel mind egyforma magasak voltak -
akkor a tetejük egy szinten volt, az uralkodó alatt:

A háromszögek szerettek bukfencezni és a fejükre állni. Felmásztak a legfelső sorba, és úgy álltak a sarkon, mint akrobaták.
És már tudjuk – amikor a felsőjükkel pontosan egy sorban állnak,
akkor a talpuk is vonalzót követ - mert ha valaki egyforma magas, akkor fejjel lefelé is egyforma!

Mindenben egyformák voltak - azonos magasságúak és ugyanazok a talpak,
és az oldalsó csúszdák - az egyik meredekebb, a másik laposabb - azonos hosszúságúak
és ugyanolyan lejtésűek. Hát csak ikrek! (csak különböző ruhákban, mindegyiknek megvan a maga kirakós darabja).

- Hol van a háromszögeknek azonos oldala? Hol egyformák a sarkok?

A háromszögek a fejükre álltak, ott álltak, és úgy döntöttek, lecsúsznak és lefekszenek az alsó sorba.
Lecsúsztak-csúsztak egy dombról; de a csúszdáik ugyanazok!
Így pontosan elfértek az alsó háromszögek között, hézag nélkül, és senki nem lökött félre senkit.

Körülnéztünk a háromszögek között, és egy érdekes vonást vettünk észre.
Ahol a szögeik összeérnek, mindhárom szög biztosan találkozik:
a legnagyobb a „fejszög”, a legélesebb szög és a harmadik, közepesen legnagyobb szög.
Még színes szalagokat is kötöttek, hogy azonnal kiderüljön, melyik melyik.

És kiderült, hogy a háromszög három szöge, ha kombinálja őket -
hozzon létre egy nagy szöget, egy „nyitott sarkot” - mint egy nyitott könyv borítóját,

_______________________O ___________________________

fordult szögnek hívják.

Bármely háromszög olyan, mint egy útlevél: három szög együtt egyenlő a kihajtott szöggel.
Valaki kopogtat az ajtódon: - kopp-kop, háromszög vagyok, hadd töltsem az éjszakát!
És mondd meg neki... Mutasd meg a szögek összegét kiterjesztett formában!
És azonnal kiderül, hogy ez egy valódi háromszög vagy egy csaló.
Sikertelen ellenőrzés - Fordulj meg száznyolcvan fokot és menj haza!

Amikor azt mondják, hogy "fordulj 180°-kal", az azt jelenti, hogy hátra kell fordulni és
menjen az ellenkező irányba.

Ugyanez ismerősebb kifejezésekben, a „volt egyszer” nélkül:

Végezzük el az ABC háromszög párhuzamos fordítását az OX tengely mentén
vektorhoz AB megegyezik az AB alap hosszával.
A háromszögek C és C 1 csúcsain áthaladó DF egyenes
párhuzamos az OX tengellyel, ami annak köszönhető, hogy merőleges az OX tengelyre
h és h 1 szakaszok (egyenlő háromszögek magassága) egyenlők.
Így az A 2 B 2 C 2 háromszög alapja párhuzamos az AB alappal
és hosszában egyenlő vele (mivel a C 1 csúcsot C-hez képest AB mennyiséggel toljuk el).
Az A 2 B 2 C 2 és az ABC háromszögek három oldala egyenlő.
Ezért az egyenes szöget alkotó ∠A 1 ∠B ∠C 2 szögek egyenlőek az ABC háromszög szögeivel.
=> Egy háromszög szögeinek összege 180°

A mozdulatokkal - „fordításokkal” az úgynevezett bizonyítás rövidebb és világosabb,
még egy gyerek is megérti a mozaik darabjait.

De a hagyományos iskola:

a párhuzamos vonalakon levágott belső keresztirányú szögek egyenlősége alapján

értékes, mert képet ad arról, miért van ez így,
Miért egy háromszög szögeinek összege egyenlő a fordított szöggel?

Mert különben a párhuzamos egyenesek nem rendelkeznének a világunk számára ismert tulajdonságokkal.

A tételek mindkét irányban működnek. A párhuzamos egyenesek axiómájából az következik
a keresztben fekvő és függőleges szögek egyenlősége, és belőlük - a háromszög szögeinek összege.

De ennek az ellenkezője is igaz: amíg a háromszög szögei 180°-osak, addig vannak párhuzamos egyenesek
(úgy, hogy egy olyan ponton keresztül, amely nem fekszik egy egyenesen, meg lehet húzni az adott egy egyedi || egyenesét).
Ha egy napon megjelenik egy háromszög a világban, amelynek szögeinek összege nem egyenlő a kibontott szöggel -
akkor a párhuzamosak megszűnnek párhuzamosak lenni, az egész világ meggörbül és elferdül.

Ha háromszög alakú csíkokat helyeznek egymás fölé -
a teljes mezőt lefedheti ismétlődő mintával, például padlólap csempével:

egy ilyen rácson különböző alakzatokat követhet nyomon - hatszögeket, rombuszokat,
csillag sokszögeket, és szerezzen be különféle parkettákat

A sík parkettával való burkolása nem csak szórakoztató játék, hanem releváns matematikai probléma is:

________________________________________ _______________________-------__________ ________________________________________ ______________
/\__||_/\__||_/\__||_/\__||_/\__|)0(|_/\__||_/\__||_/\__||_/\__||_/\=/\__||_/ \__||_/\__||_/\__||_/\__|)0(|_/\__||_/\__||_/\__||_/\__||_/\

Mivel minden négyszög téglalap, négyzet, rombusz stb.
két háromszögből állhat,
rendre egy négyszög szögeinek összege: 180° + 180° = 360°

Az azonos egyenlő szárú háromszögeket különböző módon hajtjuk négyzetekké.
2 részből álló kis négyzet. 4-es átlag. És a legnagyobb a 8 közül.
Hány figura van a 6 háromszögből álló rajzon?

Célok és célkitűzések:

Nevelési:

ismételje meg és általánosítsa a háromszöggel kapcsolatos ismereteket;
bizonyítsa be a tételt a háromszög szögeinek összegéről;
gyakorlatilag ellenőrizze a tétel megfogalmazásának helyességét;
megtanulják alkalmazni a megszerzett ismereteket a problémák megoldása során.

Nevelési:

fejleszti a geometriai gondolkodást, a tantárgy iránti érdeklődést, a tanulók kognitív és kreatív tevékenységét, a matematikai beszédet, valamint az önálló tudásszerzés képességét.

Nevelési:

fejleszteni kell a tanulók személyes tulajdonságait, mint például az elszántságot, a kitartást, a pontosságot és a csapatmunkára való képességet.

Felszerelés: multimédiás projektor, színes papírból készült háromszögek, „Élő matematika” oktatási komplexum, számítógép, képernyő.

Előkészületi szakasz: A tanár azt a feladatot adja a tanulónak, hogy készítsen történelmi jegyzetet a „Háromszög szögeinek összege” tételről.

Az óra típusa: új anyagok tanulása.

Az órák alatt

I. Szervezési mozzanat

Üdvözlet. A tanulók munkához való pszichológiai hozzáállása.

II. Bemelegít

A geometriai alakzat „háromszöggel” az előző leckéken ismerkedtünk meg. Ismételjük meg, mit tudunk a háromszögről?

A tanulók csoportokban dolgoznak. Lehetőséget kapnak arra, hogy kommunikáljanak egymással, mindegyik önállóan építse fel a megismerési folyamatot.

Mi történt? Minden csoport megteszi a javaslatait, a tanár felírja a táblára. Az eredmények megvitatása:

1. kép

III. Az óra céljának megfogalmazása

Tehát már elég sokat tudunk a háromszögről. De nem az összes. Mindegyikőtök asztalán van háromszög és szögmérő. Ön szerint milyen problémát tudunk megfogalmazni?

A tanulók megfogalmazzák az óra feladatát - egy háromszög szögeinek összegét megtalálni.

IV. Új anyag magyarázata

Gyakorlati rész(elősegíti az ismeretek és az önismereti készségek frissítését) Mérje meg a szögeket szögmérővel, és keresse meg az összegüket! Az eredményeket írja le a füzetébe (hallgassa meg a kapott válaszokat). Megtudjuk, hogy a szögek összege mindenkinél más és más (ez azért fordulhat elő, mert a szögmérőt nem pontosan alkalmazták, a számítást hanyagul végezték el stb.).

Hajtsd végig a szaggatott vonalak mentén, és nézd meg, mi mással egyenlő egy háromszög szögeinek összege:

A)
2. ábra

b)
3. ábra

V)
4. ábra

G)
5. ábra

d)
6. ábra

A gyakorlati feladat elvégzése után a tanulók megfogalmazzák a választ: Egy háromszög szögeinek összege megegyezik a kibontott szög mértékével, azaz 180°-kal.

Tanár: A matematikában a gyakorlati munka csak valamiféle állítást tesz lehetővé, de azt bizonyítani kell. Tételnek nevezzük azt az állítást, amelynek érvényességét bizonyítás állapítja meg. Milyen tételt fogalmazhatunk meg és bizonyíthatunk?

Diákok: Egy háromszög szögeinek összege 180 fok.

Történelmi hivatkozás: A háromszög szögösszegének tulajdonságát az ókori Egyiptomban állapították meg. A modern tankönyvekben leírt bizonyítást Proklosz Euklidész elemeihez írt kommentárja tartalmazza. Proklosz azt állítja, hogy ezt a bizonyítékot (8. ábra) a pitagoreusok fedezték fel (Kr. e. 5. század). Az Elemek első könyvében Eukleidész a háromszög szögeinek összegére vonatkozó tétel egy másik bizonyítását állítja fel, amely rajz segítségével könnyen megérthető (7. ábra):

7. ábra

8. ábra

A rajzok kivetítőn keresztül jelennek meg a képernyőn.

A tanár felajánlja a tétel rajzok segítségével történő bizonyítását.

Ezután a bizonyítást az „Élő matematika” tanítási és tanulási komplexum segítségével hajtják végre.. A tanár a tétel bizonyítását kivetíti a számítógépre.

Tétel a háromszög szögeinek összegéről: „A háromszög szögeinek összege 180°”

9. ábra

Bizonyíték:

A)

10. ábra

b)

11. ábra

V)

12. ábra

A tanulók röviden jegyzik fel a tétel bizonyítását a füzetükbe:

Tétel: Egy háromszög szögeinek összege 180°.

13. ábra

Adott:Δ ABC

Bizonyít: A + B + C = 180°.

Bizonyíték:

Amit bizonyítani kellett.

V. Phys. Csak egy perc.

VI. Az új anyag magyarázata (folytatás)

A háromszög szögeinek összegére vonatkozó tételből származó következtetést a tanulók önállóan vezetik le, ez hozzájárul a saját nézőpont megfogalmazásának, kifejezésének és érvelésének képességének fejlődéséhez:

Bármely háromszögben vagy minden szög hegyesszögű, vagy kettő hegyesszög, a harmadik pedig tompa vagy derékszögű..

Ha egy háromszögnek minden hegyesszöge van, akkor ún hegyesszögű.

Ha egy háromszög egyik szöge tompaszögű, akkor azt ún tompaszögű.

Ha egy háromszög egyik szöge derékszögű, akkor ún négyszögletes.

A háromszög szögeinek összegére vonatkozó tétel lehetővé teszi, hogy a háromszögeket ne csak oldalak, hanem szögek szerint is osztályozzuk. (Miközben a tanulók bemutatják a háromszögtípusokat, a tanulók kitöltik a táblázatot)

Asztal 1

Háromszög nézet	Egyenlő szárú	Egyenlő oldalú	Sokoldalú
Négyszögletes
Tompa
Hegyesszögű

VII. A tanult anyag konszolidációja.

Problémák megoldása szóban:

(A rajzok kivetítőn keresztül jelennek meg a képernyőn)

Feladat 1. Keresse meg a C szöget!

14. ábra

2. feladat Keresse meg az F szöget.

15. ábra

3. feladat Keresse meg a K és N szögeket!

16. ábra

4. feladat Keresse meg a P és T szögeket!

17. ábra

Oldja meg saját maga a 223 (b, d) feladatot.
Oldja meg a feladatot a táblán és a füzetekben, 224. sz. tanuló!
Kérdések: Lehet-e egy háromszögnek: a) két derékszöge; b) két tompaszög; c) egy derékszögű és egy tompaszög.
(szóban történik) Az egyes asztalokon lévő kártyákon különböző háromszögek láthatók. Határozza meg szemmel az egyes háromszögek típusát!

18. ábra